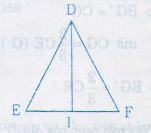
Cho tam giác DEF cân tại D với đường trung tuyến DI.
a) Chứng minh tam giác DIE và DIF.
b) Cho biết số đo của 2 góc DIE và DIF.
c) Biết DE=DF=13 cm, EF=10 cm, hãy tính độ dài đường trung tuyến DI
Cho tam giác DEF cân tại D với đường trung tuyến DI
a) Chứng minh \(\Delta DEI=\Delta DFI\)
b) Cho biết số đo của hai góc DIE và DIF
c) Biết DE = DF = 13 cm, EF = 10 cm. Hãy tính độ dài đường trung tuyến DI ?
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)

b) Vì ∆DEI = ∆DFI => ˆDIE=ˆDIFDIE^=DIF^
mà ˆDIE+ˆDIFDIE^+DIF^ = 1800 ( kề bù)
nên ˆDIE=ˆDIFDIE^=DIF^ = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
Cho tam giác DEF cân tại D với đường trung tuyến DI
a) CM tam giác DEI = tam giác DFI
b) Cho biết số đo của hai góc DIE và DIF
c) Biết DE=DF=13cm , EF=10cm , hãy tính độ dài đường trung tuyến DI
d) Gọi G là trọng tâm . Tính DG
e) Gọi M là trung điểm của DF . CMR : E,G,M thẳng hàng
Giúp mình câu d , e với ạ
d: Xét ΔDEF có
DI là trung tuyến
G là trọng tâm
=>DG=2/3DI=2/3*12=8cm
e: Xét ΔDEF có
G là trọng tâm
EM là trung tuyến
=>E,G,M thẳng hàng
Cho tam giác DEF cân tại D với đường trung tuyến DI
a) Chứng minh tam giác DEI=tam giácDFI
b) Cho biết số đo hai góc DIE và DIF
c) Biết DE=DF=13cm,EF=10cm,hãy tính độ dài đường trung tuyến DI
cho tam giác DEF cân tại D với đường trung tuyến DI
a/ chứng minh rằng tam giác DEI = tam giác DFI
b/ cho biết số đo của hai góc DIE và DIF
c/ biết DE=DF=13cm,EF=10cm , hãy tính độ dài đường trung tuyến DI
Gỉai
Tự vẽ
a)Xét tam giác DEI và tam giác DFI có :
DI cùng
Góc E=Góc F
EI=FI
=> tam giác DEI=tam giác DFI(cgc)
b)vì tam giác DEI=tam giác DFI=>góc E= góc F
vì tam giác DEF cân tại D nên DIvuông góc vs EF
=> Góc E = Góc F = 90*
c)Đinh li pytago ta có : EI=FI=EF\2=10/2=5cm
=> DI^2=DE^2-EI^2=>DI^2=13^2-5^2=144=12^2
=> DI=12
Bôi đen dãy số dưới đây :
9966699999966699999966699966669996699999996699666996699 9966999999996999999996666996699666699666996699666996699 9966699999999999999966666699996666699666996699666996699 9966666999999999999666666669966666699666996699666996699 9966666669999999966666666669966666699666996699666996699 9966666666699996666666666669966666699666996699666996666
9966666666669966666666666669966666699999996699999996699
Bấm : F3
Rồi ấn số 9 sẽ có 1 điều bất ngờ e ghé cô này đẹp hk hehehe tặng bn iu
1/Cho tam giác DEF cân tại D với đường trung tuyến DI.
a) Chứng minh ΔDEI = ΔDFI.
b)Các góc DIE và góc DIF là những góc gì?
c.biết DI=12 cm, EF=10 cm. tính độ dài cạnh DE
giúp với
xét ΔDIE và ΔDIF có :
\(DB=DE\left(gt\right)\\ \widehat{DEI}=\widehat{DFI}\left(tgD\text{EF}c\text{â}nt\text{ại}D\right)\\ DI:chung\)
=> ΔDIE = ΔDIF (c.g.c )
=> góc DIE = góc DFI ( 2 góc t.ư)
có tg DEF cân tại D , đường trung tuyến DI
=> DI là đường trung trực
=> \(\widehat{DIE}=\widehat{D\text{IF}}=\dfrac{180^O}{2}=90^O\)
=> 2 GÓC là góc vuông
C) có tg DIE = tg DIF (cmt)
=> EI = FI ( 2 CẠNH t/ư)
=> EI = FI =1/2EF = 10:2 = 5 cm
có DEI là tg vuông tại I ( I là đường trung trực của tg DEF )
ADĐL P-T-G vào tg vuông DIE ta có
\(EI^2+ID^2=DE^2\\
\Leftrightarrow DE^2=12^2+5^2\\
\Leftrightarrow DE^2=169\\
\Leftrightarrow DE=13cm\)
cho tam giác ABC vuông ở A, có góc C=30 độ AH vuông góc với BC.( H thuộc BC) .Trên đoạn HC lấy điểm D sao cho HD=HB. từ C kẽ CE vuông với AD. chứng minh rằng:
A. tam giác ABD là tam giác đều
B. AH=CE
C. EH//AC
giúp mik với mik đg cần gấp![]()
Cho tam giác DEF cân tại D với đườngtrung tuyến DI.
a/ Chứng minh tam giác DEI = tam giác DFI.
b/ Cho biết số đo của hai góc DIE và DIF.
c/ Biết DE = DF =13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.
a/ Ta có Di là đường trung tuyến nên góc EDI=FDI
Xét tam giác DEI và tam giác DFI có:
Góc EDI=FDI(cmt)
DE=DF(tam giác DEF cân tại D)
Góc E=F(tam giác DEF cân tại D)
=> Tam giác DEI=DFI(g-c-g)
a/ Ta có Di là đường trung tuyến nên góc EDI=FDI
Xét tam giác DEI và tam giác DFI có:
Góc EDI=FDI(cmt)
DE=DF(tam giác DEF cân tại D)
Góc E=F(tam giác DEF cân tại D)
=> Tam giác DEI=DFI(g-c-g)
b/ Vì tam giác DEI=tam giác DFI nên góc DIE=DIF=1/2*180=90 độ nha bạn!
c/ Ta có tam giác DEI=DFI(câu a) => EI=IF(cạnh tương ứng)
=> EI=IF=1/2*EF=1/2*10=5 cm
Áp dụng định lí Pytago vào tam giác vuông DIE ta có:
DE^2=DI^2+IE^2 =>DI^2=DE^2-IE^2=13^2-5^2=144 => DI=\(\sqrt{144}=12cm\)
tui nha
Cho tam giác DEF cân tại D với đường trung tuyến DI.
a) Chứng minh tam giac DEI va tam giac DFI b) Các góc DIE và DFIlà những góc gì?
c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.
a) Xét ΔDEI và ΔDFI có
DE=DF(ΔDEF cân tại D)
DI chung
EI=FI(I là trung điểm của EF)
Do đó: ΔDEI=ΔDFI(c-c-c)
b) Ta có: ΔDEI=ΔDFI(cmt)
nên \(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
Vậy: Các góc DIE và DIF là các góc vuông)
c) Ta có: I là trung điểm của EF(gt)
nên \(EI=\dfrac{EF}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔDEI vuông tại I, ta được:
\(DE^2=EI^2+DI^2\)
\(\Leftrightarrow DI^2=DE^2-EI^2=13^2-5^2=144\)
hay DI=12(cm)
Vậy: DI=12cm
Cho tam giác DEF cân tại D với đường trung tuyến DI.
a) Cm: Tam giác DEI = Tam giác DFI
b) Các góc DIE và góc DIF là những góc gì?
c) Biết DE = DF = 13cm, EF = 10cm. Hãy tính độ dài đường trung tuyến DI.
a) Tam giác DEI và DFI có
DE = DF (gt)
EI = FI (gt)
DI chung
=> Tam giác DEI = tam giác DFI (trường hợp bằng nhau C-C-C)
b) Theo câu a, Tam giác DEI = tam giác DFI => góc DIE = góc DFI
Vì EIF thẳng hàng => góc DIE + góc DFI = 1800 , mà 2 góc này bằng nhau
=> góc DIE = góc DFI = 180o /2 = 90o (góc vuông)
c) EF = 10 => EI = 10/2 = 5
Xét tam giác DIE vuông ở I:
DI2 + EI2 = DE2 (Định lý Pitago)
DI2 + 52 = 132
DI2 = 169 - 25 =144 = 122
=> DI = 12 cm
Cho tam giác DEF cân tại D,có đường trung tuyến DI
a, chứng minh tam giác DIE = tam giác DIF
b, 2 góc DIE và DIF là những góc gì ?
c, Cho DE=DF=13 cm, EF=10 cm. Gọi G là trọng tâm của tam giác DEF. Tính cạnh DG
a/ xét /\ DEF cân tại D
=> DE = DF (t/c /\ cân )
DI là trung tuyến
=> DI vuông với FE => DIE = 90* => DIF kề bù với DIE => DIF = 90* (1)
=> I là trung điểm EF
Xét /\ DIF và /\ DIE có :
DIF = DIE (cmt )
DF =DE (cmt)
IF = IE ( cmt )
=> /\ DIE = /\ DIF (c.g.c)
b/ (1) => DIE = DIF = 90*
=> 2 góc này là hai góc vuông
c/ chịu .