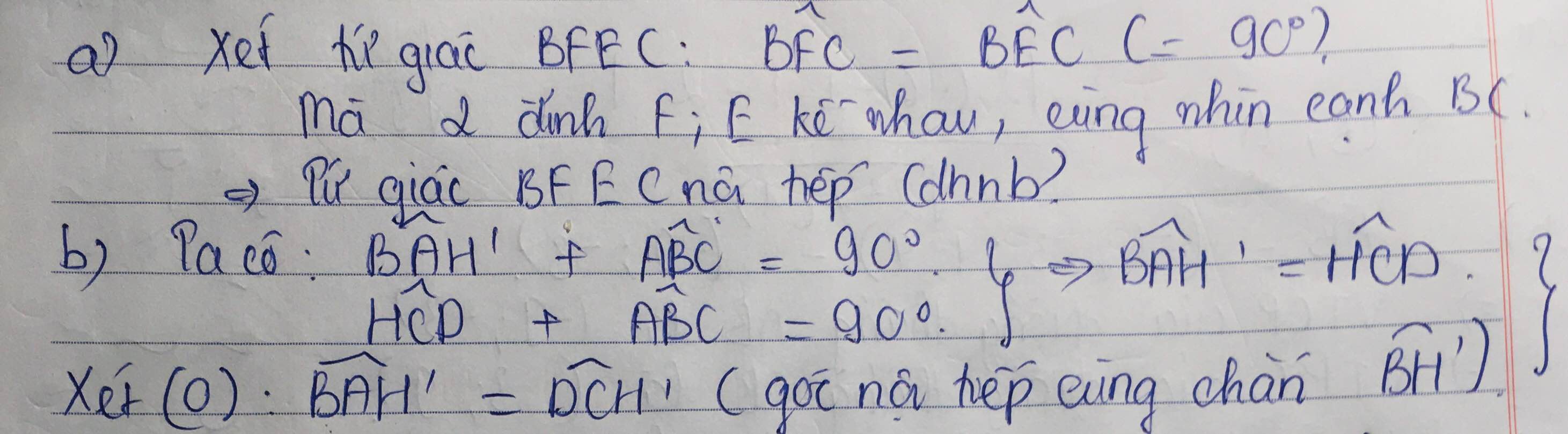giúp mình câu b, c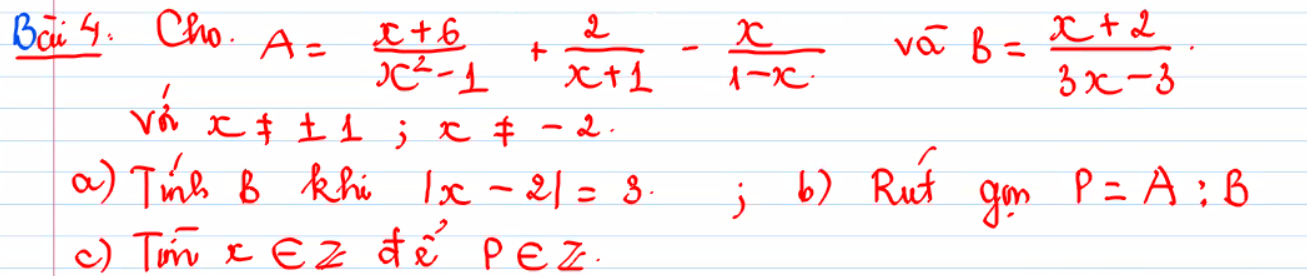

Những câu hỏi liên quan
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
mình mình  mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
ảnh kia nhiều người lắm like thế :)
Đúng 0
Bình luận (0)
Giúp mình câu b và câu c với 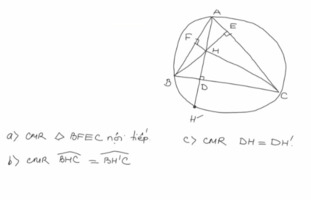
Giúp mình câu b và câu c ạ 
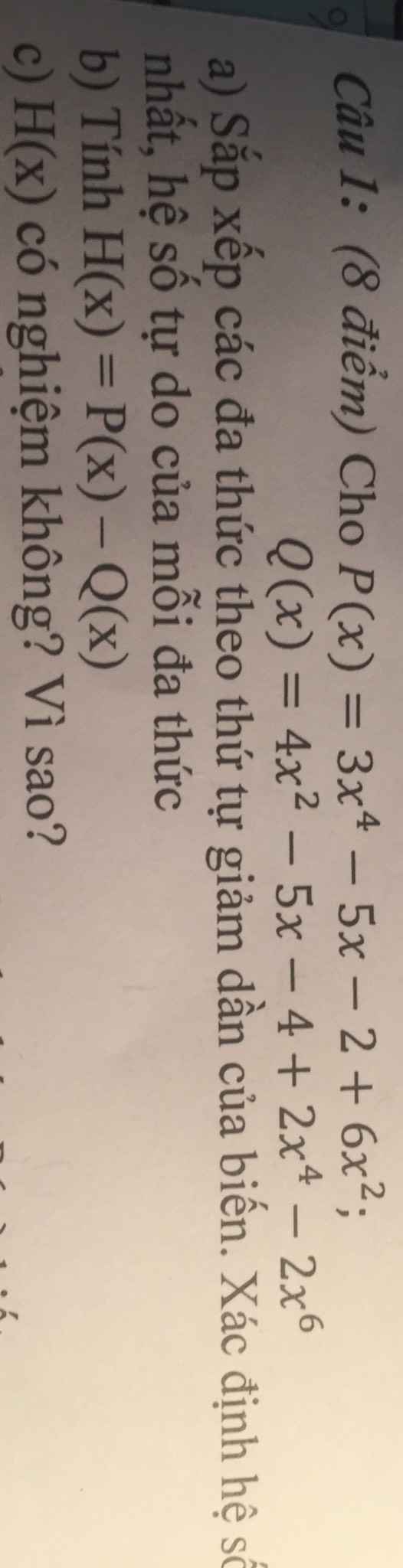
Làm giúp mình câu b với câu c với
a: P(x)=3x^4+6x^2-5x-2
Q(x)=-2x^6+2x^4+4x^2-5x-4
b: H(x)=P(x)-Q(x)
=3x^4+6x^2-5x-2+2x^6-2x^4-4x^2+5x+4
=2x^6+x^4+2x^2+2
c: H(x)=x^2(2x^4+x^2+2)+2>=2>0 với mọi x
=>H(x) ko có nghiệm
Đúng 0
Bình luận (0)
![]() giúp mình câu b,c câu 38 với mọi người
giúp mình câu b,c câu 38 với mọi người![]()


giải giúp mình câu b câu c bài 1 vs
2:
b: Khi x=-3 thì (1) sẽ là -3(m-1)+2m+5=0
=>-3m+3+2m+5=0
=>8-m=0
=>m=8
c: Để ptvn thì m-1=0
=>m=1
Đúng 1
Bình luận (0)
giúp mình câu b, c
Bài 1: Định lý talet trong tam giác:
Xét tam giác ACD có:
MI//DC(gt)
M thuộc AD; I thuộc AC
=> MD/MA=CI/AI ( định lý Talet)(1)
Xét tam giác ABC có:
IN//AB
I thuộc Ac; N thuộc BC(gt)
=> CN/BN=CI/AI( định lý talet)(2)
Từ 1,2 suy ra MD/MA=NC/NB(đpcm)
Đúng 1
Bình luận (0)

giúp mình câu b,c
a: Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right)+\dfrac{x+1}{x-1}\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1+x+1}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
Đúng 0
Bình luận (0)