\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)

Theo đề bài ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta được:

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)

\(\Rightarrow\widehat{A}=12^o.3=36^o\)

\(\widehat{B}=12^o.5=60^o\)

\(\widehat{C}=12^o.7=84^o\)

nếu số đo (độ) các góc của tam giác ABC là A , B , C (độ) thì theo điều kiện bài ra và tính chất của dãy tỉ số bằng nhau , ta có \(\dfrac{A}{3}=\dfrac{B}{5}=\dfrac{C}{7}=\dfrac{A+B+C}{3+5+7}=\dfrac{180}{15}=12\)

vậy : A = 3 . 12 = 36

B = 5 . 12 = 60

C = 7 . 12 = 84

=> A = 36 (độ) ; B = 60 (độ) ; C = 84 (độ)

Gọi số đo của các góc A,B,C trong tam giác ABC lần lượt là là a,b,c

Ta có: \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\) và tổng ba góc là 180^o

Áp dụng tính chất của dãy tỉ số bằng nhau

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{180^o}{15}=12^o\)

+) Nếu \(\dfrac{a}{3}=12\)⇒ a= 36^o

+)Nếu \(\dfrac{b}{5}\)=12⇒b=60^o

+)Nếu \(\dfrac{c}{7}\)=12⇒c=84^o

Vậy góc A bằng 36^o, góc B bằng 60^o, góc C bằng 84^o

A=36

B=60

C=84

TRỜI ! MỘT BÀI TOÁN BÙ ĐẦU BÙ ÓC

bài này lóp 7 hoc rù nhung quyen lop 7 nhình học giỏi lám đó

1.Cho tam giác ABC có số đo góc A,góc B,góc C tỉ lệ nghịch vs 3;4;6.Tính số đo các góc của tam giác ABC.

2.Cho tam giác ABC có số đo góc A,góc B,góc C tỉ lệ thuận vs 3;4;5.Tính số đo các góc của tam giác ABC.

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).

Theo định lí tổng ba góc của tam giác ta có:

    a + b + c = 180.

Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:

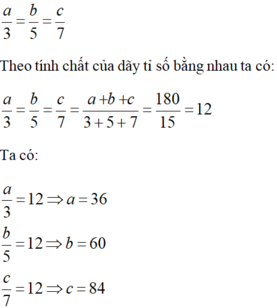
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o

Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)

Mà số đo ba góc \(\widehat A,\widehat B,\widehat C\) của tam giác ABC tỉ lệ với 5;6;7 nên \(\dfrac{{\widehat A}}{5} = \dfrac{{\widehat B}}{6} = \dfrac{{\widehat C}}{7}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\begin{array}{l}\dfrac{{\widehat A}}{5} = \dfrac{{\widehat B}}{6} = \dfrac{{\widehat C}}{7} = \dfrac{{\widehat A + \widehat B + \widehat C}}{{5 + 6 + 7}} = \dfrac{{180^\circ }}{{18}} = 10^\circ \\ \Rightarrow \widehat A = 10^\circ .5 = 50^\circ \\\widehat B = 10^\circ .6 = 60^\circ \\\widehat C = 10^\circ .7 = 70^\circ \end{array}\)

Vậy số đo 3 góc \(\widehat A,\widehat B,\widehat C\) lần lượt là \(50^\circ ;60^\circ ;70^\circ \)

`a,` Gọi số đo `3` góc của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`

Tỉ lệ thức biểu diễn mối quan hệ giữa số đo `3` góc trong Tam giác `ABC` là `x/2=y/3=z/4`

`b,` Tổng số đo `3` góc trong `1` tam giác là `180^0`

`-> x+y+z=180`

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

`x/2=y/3=z/4=(x+y+z)/(2+3+4)=180/9=20`

`-> x/2=y/3=z/4=20`

`->x=20*2=40, y=20*3=60, z=20*4=80`

Vậy, số đo của `3` góc trong Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0.`

a:

Đặt \(a=\widehat{A};b=\widehat{B};c=\widehat{C}\)

a/2=b/3=c/4

b: a/2=b/3=c/4=(a+b+c)/(2+3+4)=180/9=20

=>a=40; b=60; c=80

gọi số đo 3 góc của tam giác lần lượt là a,b,c => a+b+c = 180 độ( định lí tổng 3 góc trong tam giác

tỉ lệ với 2;3;5

=> \(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\)

                                                                     = \(\frac{a+b+c}{2+3+5}\) (tính chất dãy tỉ số bằng nhau)

                                                                      = \(\frac{180}{10}\)(do a+b+c=180 độ)

                                                                       = 18 độ

=> a = 18.2=36 độ

      b = 18.3= 54 độ

     c = 18.5 = 90 độ

Ta có: A+B+C=180*(tổng 3 góc của tam giác)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

A/2+B/3+C/5=A+B+C=2+3+5=A+B+C/10=180*:10*=18*