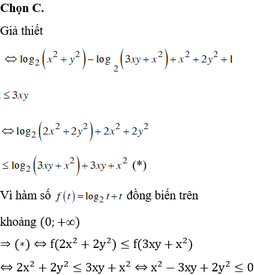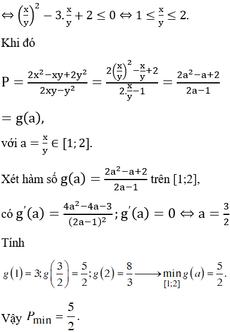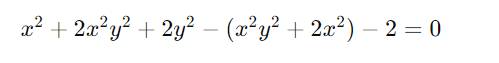tìm các số nguyen tố x,y thỏa mãn đề bài x2-2y2-1=0
Những câu hỏi liên quan
tìm các nguyên tố x,y thỏa mãn x2-2y2=1
20 tháng 7 2021 lúc 16:22
bài 1: cho các số dương x, y, z thỏa mãn x+y+z=1. Tìm min
a) A = x2+y2+z2
b) B = x2+y2+3z2
c) C=x2+2y2+3z2
d) D=x2+by2+cz2
13 tháng 1 lúc 19:35
Tìm tất cả các bội số nguyên (x;y) thỏa mãn phương trình:
a) x2 - 2x + 2y2 = 2(xy +1)
b) x2 + 2y2 + 2xy - 2x = 7
a.
\(\Leftrightarrow2x^2-4x+4y^2=4xy+4\)
\(\Leftrightarrow\left(x^2-4xy+4y^2\right)+\left(x^2-4x+4\right)=8\)
\(\Leftrightarrow\left(x-2y\right)^2+\left(x-2\right)^2=8\) (1)
Do \(\left(x-2y\right)^2\ge0;\forall x;y\)
\(\Rightarrow\left(x-2\right)^2\le8\)
\(\Rightarrow\left(x-2\right)^2=\left\{0;1;4\right\}\)
TH1: \(\left(x-2\right)^2\Rightarrow x=2\) thế vào (1)
\(\Rightarrow\left(2-2y\right)^2=8\Rightarrow\left(1-y\right)^2=2\) (ko tồn tại y nguyên t/m do 2 ko phải SCP)
TH2: \(\left(x-2\right)^2=1\Rightarrow\left(x-2y\right)^2=8-1=7\), mà 7 ko phải SCP nên pt ko có nghiệm nguyên
TH3: \(\left(x-2\right)^2=4\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\) thế vào (1):
- Với \(x=0\Rightarrow\left(-2y\right)^2+4=8\Rightarrow y^2=1\Rightarrow y=\pm1\)
- Với \(x=2\Rightarrow\left(2-2y\right)^2+4=8\Rightarrow\left(1-y\right)^2=1\Rightarrow\left[{}\begin{matrix}y=0\\y=2\end{matrix}\right.\)
Vậy pt có các cặp nghiệm là:
\(\left(x;y\right)=\left(0;1\right);\left(0;-1\right);\left(2;0\right);\left(2;2\right)\)
Đúng 2
Bình luận (0)
b.
\(\Leftrightarrow2x^2+4y^2+4xy-4x=14\)
\(\Leftrightarrow\left(x^2+4xy+4y^2\right)+\left(x^2-4x+4\right)=18\)
\(\Leftrightarrow\left(x+2y\right)^2+\left(x-2\right)^2=18\) (1)
Lý luận tương tự câu a ta được
\(\left(x-2\right)^2\le18\Rightarrow\left(x-2\right)^2=\left\{0;1;4;9;16\right\}\)
Với \(\left(x-2\right)^2=\left\{0;1;4;16\right\}\) thì \(18-\left(x-2\right)^2\) ko phải SCP nên ko có giá trị nguyên x;y thỏa mãn
Với \(\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\) thế vào (1)
- Với \(x=5\Rightarrow\left(5+2y\right)^2+9=18\Rightarrow\left(5+2y\right)^2=9\)
\(\Rightarrow\left[{}\begin{matrix}5+2y=3\\5+2y=-3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=-1\\y=-4\end{matrix}\right.\)
- Với \(x=-1\Rightarrow\left(-1+2y\right)^2=9\Rightarrow\left[{}\begin{matrix}-1+2y=3\\-1+2y=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=2\\y=-1\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(5;-1\right);\left(5;-4\right);\left(-1;3\right);\left(-1;-3\right)\)
Đúng 2
Bình luận (0)
toán 8 chứng minh không tồn tại hai số x,y thỏa mãn x2+2y2-2xy+x-2y+1=0
\(x^2+2y^2-2xy+x-2y+1=0\)
\(4x^2+8y^2-8xy+4x-8y+4=0\)
\(4x^2-4x\left(2y-1\right)+\left(2y-1\right)^2+8y^2-8y+4-\left(2y-1\right)^2=0\)
\(\left(2x-2y+1\right)^2+\left(4y^2-4y+1\right)+3=0\)
\(\left(2x-2y+1\right)^2+\left(2y-1\right)^2+3=0\) ( vô lí)
=> KL...........
Đúng 0
Bình luận (0)
Cho x,y,z là các số thực thỏa mãn:
-2≤x,y,z≤5 và x+2y+3z≤9. Tìm GTLN của bt:
M= x2 +2y2 +3z2
Cho hai số x và y thỏa mãn x2+2y2-3xy=0 và x>y>0.
Tính GTBT: A=\(\dfrac{6x+16y}{5x-3y}\)
\(x^2+2y^2-3xy=0\Leftrightarrow\left(x-y\right)\left(x-2y\right)=0\)
\(\Leftrightarrow x-2y=0\) (do \(x>y\) nên \(x-y>0\))
\(\Leftrightarrow x=2y\)
\(\Rightarrow A=\dfrac{6.2y+16y}{5.2y-3y}=\dfrac{28y}{7y}=4\)
Đúng 0
Bình luận (0)
Cho các số thực x, y dương và thỏa mãn
log
2
x
2
+
y
2
3
xy
+
x
2
+
2
log
2
x
2
+...
Đọc tiếp
Cho các số thực x, y dương và thỏa mãn log 2 x 2 + y 2 3 xy + x 2 + 2 log 2 x 2 + 2 y 2 + 1 ≤ log 2 8 xy .Tìm giá trị nhỏ nhất của biểu thức P = 2 x 2 - xy + 2 y 2 2 xy - y 2 .
16 tháng 7 2021 lúc 16:01
Tìm x ,y thỏa mãn: x2 + 2x2y2 + 2y2 - (x2y2 + 2x2) - 2 = 0 .
cac ban giup minh voi roi minh tick cho
Bạn vui lòng viết đề đầy đủ, và gõ bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 2
Bình luận (0)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y