bài toán giả thiết là gì vậy các bạn
mik cần nhé
cho hỏi là trong một bài toán về tam giác nếu hai có cạnh bằng nhau rồi thi có cần phải ghi cạnh chung không
vd:AB=AD,BC=DC(THEO GIẢ THIẾT)
AC LÀ CẠNH CHUNG
VẬY TAM GIÁC NÀY BẰNG TAM GIÁC KIA(C.C.C)
cho hỏi là cần nhất thiết phải ghi canh chung ko
Có chứ em. Nếu không ghi thì sao đủ điều kiện để hai tam giác bằng nhau theo trường hợp cạnh - cạnh - cạnh được
Đố bạn biết bài toán này nhé.
Mai nấu được ba bữa thì bạn ấy ăn được 3 bát cơm.Vậy 3 bữa nữa bạn Mai sẽ ăn bao nhiêu bát cơm?
Vậy các bạn hãy giải đi nha.Esay lun đó.Vậy các bạn có biết dạng bài toán này là dạng gì mà nó rất dễ ko?
Nhưng nếu cộng thêm ngày hôm nay thì sẽ là 12 bát
tui đang hỏi dạng toán về tỉ lệ thuận nhé.Làm gì có cộng với trừ đâu.
Quá trình giải bài toán trên máy tính gồm các bước nào? *
Xác định bài toán, xây dựng thuật toán, viết chương trình.
Xác định giả thiết kết luận của bài toán, tìm lời giải.
Tìm hiểu bài toán, xây dựng thuật toán, viết chương trình.
Xây dựng thuật toán, xác định bài toán, viết chương trình.
tìm hiểu bài,xây dựng thuật toán,viết chương chình
Em nào có bài tập cần hỏi hôm nay đăng lên rồi nhắn tin cho Thầy Giáo Toán, thầy sẽ hướng dẫn giúp.
Điều kiện để được giúp:
1. Viết bài rõ ràng, có giả thiết kết luận đầy đủ.
2. Nghiêm túc hỏi bài, chỉ hỏi những bài chưa làm được.
thầy chờ nhé
so sánh hai lũy thừa 123456789 và 567891234
toán lớp 6
giúp em bài này với ạ :
tìm x biết :
\(\sqrt{x-1}=5\) \(;\sqrt{\left(x-\frac{1}{3}\right)^2=7}\) \(;\sqrt{1+x}+5=3\)
ta có
1234^56789>1000^50000=(10^3)^50000=10^150000
56789^1234<100000^2000=(10^5)2000=10^10000
vì 150000>10000 nên 1234^56789 >56789^1234
các bn ơi trong bài hình ghi giả thiết thì có được tính điểm ko vậy
Phần giả thuyết không viết cũng được nhé mà đối với chương trình lớp 7 thì bạn nên ghi
Trong bài toán ứng dụng, khi chơi trên sân cầu lông đơn, các lần phát cầu với thông tin như sau có được xem là hợp lệ không? (Các thông tin không được đề cập thì vẫn giữ như trong giả thiết bài toán trên)
a) Vận tốc xuất phát của cầu là 12 m/s
b) Vị trí phát cầu cách mặt đất 1,3 m.
Lưu ý: Các thông số về sân cầu lông đơn được cho trong Hình 11.
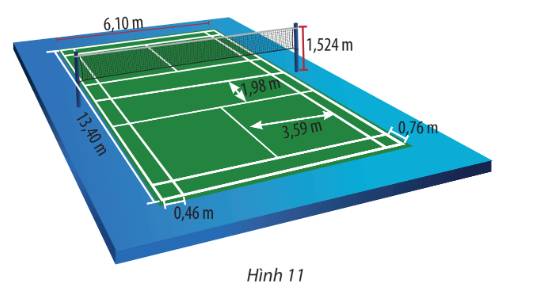
a)
Chọn hệ trục tọa độ như Hình 9 (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).
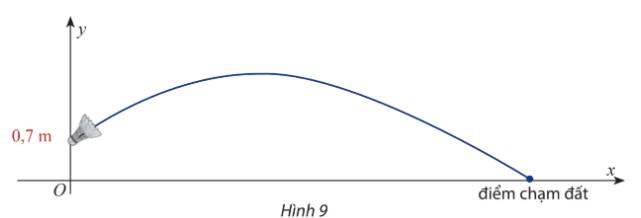
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 12\;m/s\), phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.12}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7\)
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \( - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = 0\) ta được \({x_1} \approx - 1,11\) và \({x_2} \approx 13,84\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m > 13,4 m (chiều dài cả sân)
Vậy lần phát cầu đã bị hỏng vì điểm rơi của cầu nằm ngoài đường biên ngoài.
b)
Ta so sánh tung độ của điểm trên quỹ đạo (có hoành động bằng khoảng cách từ điểm phát cầu đến chân lưới phân cách) với chiều cao mép trên của lưới.
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 8\;m/s\), vị trí phát cầu cách mặt đất 1,3 m. Phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\)
Khi \(x = 4,\)ta có \(y = - \frac{{4,9}}{{48}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 1,3 \approx 1,98 > 1,524\)
Vậy quỹ đạo của cầu cao hơn mép trên của lưới.
Tiếp theo ta kiểm tra vị trí cầu rơi có vượt đường biên ngoài hoặc chưa tới đường biên trong hay không.
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\) ta được \({x_1} \approx - 1,73\) và \({x_2} \approx 7,38\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7.38 m.
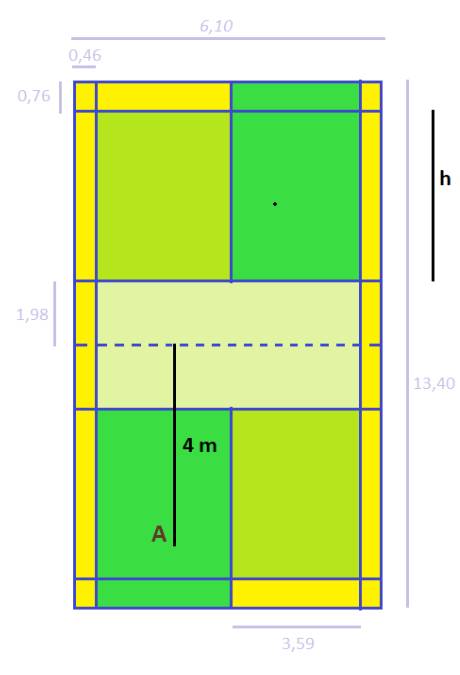
Dễ thấy: độ dài h (chiều dài của khu vực hợp lệ) là: \(13,4:2 - 1,98 -0,76= 3,96\) (m).
Do đó lần phát là hợp lệ nếu khoảng cách từ vị trí phát đến điểm rơi thuộc khoảng \(4 + 1,98 = 5,98(m)\) và \(4 + 1,98 +3,96= 9,94(m)\) và \(5,98 < 7,38 < 9,94\).
Như vậy vị trí quả cầu trên mặt đất nằm giữa đường biên trong và đường biên ngoài.
Kết luận: lần phát cầu này được coi là hợp lệ.
Cho mik hỏi:
10-/x+1/=5
Bài toán trên thuộc dạng toán gì .Mik biết cách làm rồi nhé chỉ cần biết dạng toán trên là gì thôi.
dang phuong trinh chua dau gia tri tuyet doi
đang phương trình 1 biến có chứa trị tuyệt đối
Xét bài toán:
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của MA lấy điểm E sao cho ME = MA. Chứng minh rằng AB//CE.
Dưới đây là hình vẽ và giả thiết kết luận của bài toán:
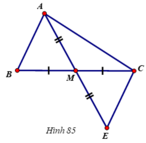
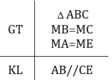
Hãy sắp xếp lại năm câu sau đây một cách hợp lí để giải bài toán trên:
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có
Lưu ý : Để cho gọn ,các quan hệ nằm giữa thẳng hàng (như M nằm giữa B ,C E thuộc tia đối của MA ) đã được thể hiện ở hình vẽ nên có thể không ghi ở phần giả thiết
- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
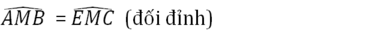
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)

Bài toán đồng hồ
Giả sử chúng ta có cái đồng hồ kim, gồm kim phút và kim giờ, và cái đồng hồ đảm bảo còn chạy đúng giờ nhé. Giả sử lúc ta xem đồng hồ ta thấy thời gian bây giờ là 3h đúng (kim giờ ngay số 3 kim phút thì ngay số 12 đó), vậy hỏi các bạn nhé sau bao nhiêu thời gian thì kim phút đuổi kịp kim giờ nhỉ?