Cho tam giác ABC cân tại A, kẻ AH vuônggóc với BC tại H.a) Chứng minh rằng ∆AHB = ∆AHCb) Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB = ID.Chứng minh ID = IC

Những câu hỏi liên quan
Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh rằng ΔAHB = ΔAHC.
b) Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB = ID. Chứng minh IB = IC, từ đó suy ra AH + BD > AB + AC.
c) Trên cạnh CI, lấy điểm E sao cho CI =2/3 CE . Chứng minh ba điểm D, E, H thẳng hàng.
a ) Xét Δ AHB và Δ AHC có :
AB = AC ( GT )
Góc AHB = góc AHC
AH là cạnh chung
=> tam giác AHB = tam giác AHC ( cạnh huyền - cạnh góc vuông )
Đúng 0
Bình luận (1)
cho tam giác ABC cân tại A kẻ AH vuông góc BC( H thuộc BC)
a, chứng minh tam giác AHB=AHC
b, gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB lấy điểm D sao cho IB=ID. cm IB=IC
từ đó cm AH+BD>AB+AC
a: Xet ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó:ΔAHB=ΔAHC
b: Xét ΔIBC có
IH là đường cao
IH là đường trung tuyến
Do đó: ΔIBC cân tại I
hay IB=IC
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.a, c/m: tam giác AHB tam giác AHCb, Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IBID. c/m IBIC, từ đó suy ra AH+BD AB+ACc, Trên cạnh CI lấy điểm E sao cho CEfrac{2}{3}CI. c/m D,E,H thẳng hàngBài 2: Cho tam giác ABC có góc A 60 độ. Tia phân gicas của góc b cái AC tại D, ia phân giác của góc C cắt AB tại e. Các tai phân giác đó cắt nhau tại I. c/m: IDIE
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a, c/m: tam giác AHB = tam giác AHC
b, Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB=ID. c/m IB=IC, từ đó suy ra AH+BD > AB+AC
c, Trên cạnh CI lấy điểm E sao cho CE=\(\frac{2}{3}\)CI. c/m D,E,H thẳng hàng
Bài 2: Cho tam giác ABC có góc A= 60 độ. Tia phân gicas của góc b cái AC tại D, ia phân giác của góc C cắt AB tại e. Các tai phân giác đó cắt nhau tại I. c/m: ID=IE
Bài 9: (3,5 điểm) Cho tam giác ABC vuông tại A, lấy điểm m là trung điểm của BC. Vẽ MH AC (H thuộc AC). Trên tia HM lấy điểm K sao cho MK MH.a) Chứng minh ΔMHC ΔMKB rồi suy ra HKB 90Chứng minh HK // AB và KB AH.Chứng minh ΔMAC cân.Gọi G là giao điểm của AM và BH. Chứng minh GB + GC 3GA.Bài 8: (3,5 điểm) Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.Chứng minh rằng ΔAHB ΔAHC.Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB ID. Chứng minh IB IC, từ...
Đọc tiếp
Bài 9: (3,5 điểm) Cho tam giác ABC vuông tại A, lấy điểm m là trung điểm của BC. Vẽ MH AC (H thuộc AC). Trên tia HM lấy điểm K sao cho MK = MH.
a) Chứng minh ΔMHC = ΔMKB rồi suy ra HKB= 90
Chứng minh HK // AB và KB = AH.
Chứng minh ΔMAC cân.
Gọi G là giao điểm của AM và BH. Chứng minh GB + GC > 3GA.
Bài 8: (3,5 điểm) Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
Chứng minh rằng ΔAHB = ΔAHC.
Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB = ID. Chứng minh IB = IC, từ đó suy ra AH + BD > AB + AC.
Trên cạnh CI, lấy điểm E sao cho CE 23 CI. Chứng minh ba điểm D, E, H thẳng hàn
Bài 5: Cho ΔABC cân tại A, A= 90. vẽ AH vuông góc với BC tại H.
a) Chứng minh: ΔABH = ΔACH
b) Cho biết AH = 4cm; BH = 3cm. Tính độ dài cạnh AB.
c) Qua H, vẽ đường thẳng song song với AC cắt cạnh AB tại M. Gọi G là giao điểm của CM và AH. Chứng minh G là trọng tâm của ΔABC và tính độ dài cạnh AG.
(Vẽ hình giúp mk với nha mk cần gấp ạ)
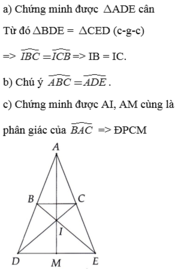
Bài 1. Cho tam giác ABC cân tại A ( góc A 90°). Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc vói AB tại E.a) Chứng minh tam giác ADE cân.b) Chứng minh DE// BC.c) Gọi I là giao điểm của BD và CE. Chứng minh IB ICd) Chứng minh. AI vuông góc BC.Bài 2. Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D trên tia đối của tia CA lấy điểm E sao cho BD CE, Gọi I là giao điểm của BE và CD.a) Chứng minh IB IC, ID IE.b) Chứng minh DE // BC.c) Gọi M là trung điểm của BC. Chứng minh ba điểm A...
Đọc tiếp
Bài 1. Cho tam giác ABC cân tại A ( góc A< 90°). Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc vói AB tại E.
a) Chứng minh tam giác ADE cân.
b) Chứng minh DE// BC.
c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC
d) Chứng minh. AI vuông góc BC.
Bài 2. Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D trên tia đối của tia CA lấy điểm E sao cho BD = CE, Gọi I là giao điểm của BE và CD.
a) Chứng minh IB = IC, ID = IE.
b) Chứng minh DE // BC.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng
Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D trên tia đối của tia CA lấy điểm E sao cho BD = CE, Gọi I là giao điểm của BE và CD.
a) Chứng minh IB = IC, ID = IE.
b) Chứng minh DE // BC.
c) Gọi M là trung điểm của BC. Chứng minh ba điểm A, M, I thẳng hàng.
cho tam giác abc cân tại A. Kẻ AH vuông góc BC9 HϵBC, Trên tia AH lấy E sao cho H là trung điểm của AE. Trên tia đối của tia CB lấy điểm F sao cho CF=BC. gọi m là trung điểm của EF
a)chứng minh tam giác abc= ahc
b)chứng minh acm thẳng hàng
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAEF có
FH là đường trung tuyến
FC=2/3FH
Do đó: C là trọng tâm của ΔAEF
=>AC là đường trung tuyến ứng với cạnh FE
mà M là trung điểm của FE
nên A,C,M thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A Trên tia đối của tia BA lấy điểm D Trên tia đối của tia CA lấy điểm E sao cho BD = CE Gọi I là giao điểm của BE và CD
a) Chứng minh rằng IB=IC,ID=IE
b) Chứng minh rằng BC song song với d e
c) Gọi M là trung điểm của BC chứng minh rằng ba điểm A,M,I thẳng hàng
a, đơn giản ta CM được hai tam giác DCB và EBC bằng nhau => góc EBC = góc DCB => tam giác BIC cân tại I => IB = IC (đpcm)
tương tự chứng minh được hai tam giác DIB và EIC bằng nhau => ID = IE (đpcm)
b, ta có tam giác DAE cân tại A => 2góc D = 180o -góc A
tam giác BAC cân tại A => 2 góc B = 180o - góc A
=> góc D = góc B => BC// DE (đpcm)
c, Nối AM => AM vừa là trung tuyến vừa là đường trung trựctại M của BC
Nối IM => IM vừ là trung tuyến vừa là đường trung trực tại M của BC
=> AM và IM cùng nằm trên đường trung trực của BC tại M hay 3 điểm A,M,I thẳng hàng
Đúng 0
Bình luận (0)
a) Tam giác ABC cân tại A suy ra \(\widehat{B_1}=\widehat{C_1}\)
Xét tam giác ABM và tam giác ACM có :
AB = AC ( tam giác ABC cân tại A )
\(\widehat{B_1}=\widehat{C_1}\left(cmt\right)\)
BM = CM ( gt )
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\)
Xét tam giác ABI và tam giác ACI có :
AI chung
AB = AC ( tam giác ABC cân tại A )
\(\widehat{A_1}=\widehat{A_2}\left(cmt\right)\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c-g-c\right)\)
\(\Rightarrow IB=IC\)
Vì AD = AB + BD
AE = AC + BC
Mà AB = AC ( tam giác ABC cân tại A )
DB = EC ( gt )
\(\Rightarrow AD=AE\)
Xét tam giác ADI và tam giác AEI có :
AI chung
AD = AE ( cmt )
\(\widehat{A_1}=\widehat{A_2}\left(cmt\right)\)
\(\Rightarrow\Delta ADI=\Delta AEI\left(c-g-c\right)\)
\(\Rightarrow DI=EI\)hay ID = IE
b) Vì tam giác ABC cân tại A ( gt )
\(\Rightarrow\)\(\widehat{B_1}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Vì tam giác ADE có AD = AE ( cmt )
Suy ra tam giác ADE cân
\(\Rightarrow\widehat{D}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{B_1}=\widehat{D}\)mà hai góc này ở vị trí đồng vị
Suy ra BC // DE
c) Ta có : \(\widehat{M_2}=\widehat{M_1}\left(\Delta ABM=\Delta ACM\right)\left(cmt\right)\)
Mà \(\widehat{M_1}+\widehat{M_2}=180^o\)( 2 góc này ở vị trí kề bù )
\(\widehat{M_2}=\widehat{M_3}\)( đối đỉnh )
\(\Rightarrow\widehat{M_1}+\widehat{M_3}=180^o\)
\(\Rightarrow\)A ; M ; I thẳng hàng
Đúng 2
Bình luận (0)
cho tam giác ABC cân tại A . trên tia đối của tia BA lấy điểm D trên tia đối của tia CA láy điểm E sao cho BD=CE , gọi I là giao điểm của BE , CD
A , chứng minh IB=IC , ID=IE
B, chứng minh DE//BC
C, gọi M là trung điểm của BC. chứng minh 3 điểm A,M,I thẳng hàng
a: Ta có: \(\widehat{ABC}+\widehat{DBC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{BCE}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{DBC}=\widehat{BCE}\)
Xét ΔDBC và ΔECB có
BD=CE
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>DC=EB
ΔDBC=ΔECB
=>\(\widehat{BCD}=\widehat{CBE}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>IB=IC
Ta có: IB+IE=BE
IC+ID=CD
mà IB=IC và BE=CD
nên IE=ID
b: Xét ΔABC có \(\dfrac{AB}{BD}=\dfrac{AC}{CE}\)
nên BC//DE
c: Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(2)
Ta có: IB=IC
=>I nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,M,I thẳng hàng
Đúng 1
Bình luận (0)