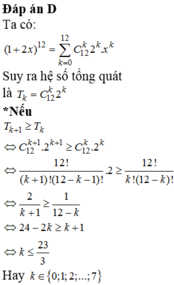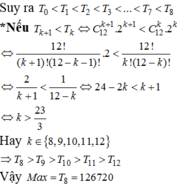Tifm hệ số lớn nhất trong khia triển thành đa thức của (1/3+3/4x)4

Những câu hỏi liên quan
Tìm hệ số lớn nhất trong các hệ số của các số hạng khi khai triển nhị thức sau thành đa thức (1+x)101
Giúp với ạ
Hệ số lớn nhất sẽ tương ứng với số hạng đứng chính giữa
=>Hệ số lớn nhất là \(C^{51}_{101}\)
Đúng 2
Bình luận (0)
Hệ số có giá trị lớn nhất khi khai triển P x = 1 + 2 x 12 thành đa thức là
A. 162270
B. 126720
C. 126270
D. 126720
Tìm hệ số của x13 trong khai triển \(f\left(x\right)=\left(\dfrac{1}{4}+x+x^2\right)^3\left(2x+1\right)^{15}\) thành đa thức
\(f\left(x\right)=\sum\limits^3_{i=0}C_3^i\left(x+x^2\right)^i.\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k\left(2x\right)^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}C_3^i.C_i^jx^j.\left(x^2\right)^{i-j}\left(\dfrac{1}{4}\right)^{3-i}\sum\limits^{15}_{k=0}C_{15}^k.2^k.x^k\)
\(=\sum\limits^3_{i=0}\sum\limits^i_{j=0}\sum\limits^{15}_{k=0}C_3^iC_i^jC_{15}^k\left(\dfrac{1}{4}\right)^{3-i}.2^k.x^{2i+k-j}\)
Số hạng chứa \(x^{13}\) thỏa mãn:
\(\left\{{}\begin{matrix}0\le i\le3\\0\le j\le i\\0\le k\le15\\2i+k-j=13\end{matrix}\right.\)
\(\Rightarrow\left(i;j;k\right)=\left(0;0;13\right);\left(1;0;12\right);\left(1;1;11\right);\left(2;0;11\right);\left(2;1;10\right);\left(2;2;9\right);\left(3;0;10\right);\left(3;1;9\right)\)
\(\left(3;2;8\right);\left(3;3;7\right)\) (quá nhiều)
Hệ số....
Đúng 1
Bình luận (0)
phân tích đa thức A thành tích của 1 nhị thức bậc nhất vs 1 đa thức bậc 3 với hệ số nguyên sao cho hệ số cao nhất của đa thức bậc ba là 1:A=3x^4+11x^3-7x^2-2x+1
1. Phân tích đa thức thành nhân tử
B=(x-y)^3 + (y-z)^3 + (z-x)^3 ( phương pháp xét giá trị riêng)
2. Cho đa thức hãy phân tích Y thành tidch của 1 đa thức bậc nhất với 1 đa thức bậc 3 có hệ số nguyên sao cho hệ số cao nhất của đa thức bậc 3 là 1
Y= 3x^4 + 11x^3 - 7x^2 - 2x + 1 (pp dùng hệ số bất định)
câu 1 : tìm bậc, hệ số cao nhất và hệ số tự do của đa thức : P-x^3-2x^2+x^3+4x+5
câu 2 xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau :
a) 5x^2-2x+1-3x^4
b) 1,5x^2-3,4x^4+0,5x^2-1
câu 3 :
a) Tính left(dfrac{1}{2}x^3right)timesleft(-4x^2right). tìm hệ số và bậc của đơn thức nhận được
b) Tính dfrac{1}{2}x^3-dfrac{5}{2}x^3. tìm hệ số và bậc của đơn thức nhận được
câu 4 : cho 2 đa thức :
Aleft(xright)x^3+dfrac{3}{2}x-7x^4+dfrac{1}{2}x-4x^2+9 và Bleft(xright)x^5-3x^2+8x^4-5x...
Đọc tiếp
câu 1 : tìm bậc, hệ số cao nhất và hệ số tự do của đa thức : \(P=-x^3-2x^2+x^3+4x+5\)
câu 2 xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau :
a) \(5x^2-2x+1-3x^4\)
b) \(1,5x^2-3,4x^4+0,5x^2-1\)
câu 3 :
a) Tính \(\left(\dfrac{1}{2}x^3\right)\times\left(-4x^2\right)\). tìm hệ số và bậc của đơn thức nhận được
b) Tính \(\dfrac{1}{2}x^3-\dfrac{5}{2}x^3\). tìm hệ số và bậc của đơn thức nhận được
câu 4 : cho 2 đa thức :
\(A\left(x\right)=x^3+\dfrac{3}{2}x-7x^4+\dfrac{1}{2}x-4x^2+9\) và \(B\left(x\right)=x^5-3x^2+8x^4-5x^2-x^5+x-7\)
a) thu gọn và sắp xếp 2 đa thức trên theo lũy thừa giảm của biến
b) tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đã cho
câu 5 : cho 2 đa thức :
\(P\left(x\right)=5x^3+2x^4-x^2+3x^2-x^3-2x^4-4x^3\) và
\(Q\left(x\right)=3x-4x^3+8x^2-5x+4x^3+5\)
thu gọn và sắp xếp 2 đa thức trên theo lũy thừa giảm của biến
câu 6 : người ta dùng 2 máy bơm để bơm nước vào bể chứa nước. máy thứ nhất bơm mỗi giờ được \(22m^3\) nước. máy thứ 2 bơm mỗi giờ được \(16m^3\) nước. sau cả hai máy chạy trong \(x\) giờ, người ta tắt máy thứ nhất và để máy thứ 2 chạy thêm \(0,5\) giờ nữa thì bể nước đầy.
hãy viết đa thức (biến \(x\)) biểu thị dung tích của mỗi bể (\(m^3\)), biết rằng trước khi bơm trong bể có \(1,5m^3\) nước. tìm hệ số cao nhất và hệ số tự do của đa thức đó.
câu 7 : viết đa thức \(F\left(x\right)\) thỏa mãn đồng thời các điều kiện sau :
\(\cdot\) bật của \(F\left(x\right)\) bằng \(3\)
\(\cdot\) hệ số của \(x^2\) bằng hệ số của \(x\) và bằng \(2\)
\(\cdot\) hệ số cao nhất của \(F\left(x\right)\) bằng \(-6\) và hệ số tự do bằng \(3\)
câu 8 : kiểm tra câu hỏi sau :
a) \(x=\dfrac{-1}{8}\) có phải là nghiệm của đa thức \(P\left(x\right)=4x+\dfrac{1}{2}\) không
b) trong 3 số \(1;-1;2\), số nào là số nghiệm của đa thức \(Q\left(x\right)=x^2+x-2?\)
câu 9 : mẹ cho quỳnh 100 000 đồng. quỳnh mua một bộ dụng cụ học tập có giá 37 000 đồng và một cuốn sách tham khảo môn toán với giá \(x\) (nghìn đồng).
a) hãy tìm đa thức (biến \(x\)) biểu thị số tiền quỳnh còn lại (đơn vị nghìn đồng). tìm bậc của đa thức đó.
b) sau khi mua sách thì quỳnh tiêu vừa hết số tiền mẹ cho, hỏi số tiền của cuốn sách là bao nhiêu ?
Em muốn hỏi bài nào vậy? Quá nhiều bài thầy cô và các bạn không thể trả lời được hết em ạ
Đúng 1
Bình luận (1)
Bài 1. Cho đa thức: P(x)=2+〖5x〗^2-3x^3+4x^2-2x-x^3+6x^5.
a)Thu gọn và sắp xếp các hạng tử của đa thức P(x) theo lũy thừa giảm của biến.
b)Xác định bậc của đa thức P(x).
c)Xác định hệ số lớn nhất, hệ số tự do của đa thức P(x).
Tính giá trị của đa thức P(x) tại x=-1.
a: P=2+25x^2-3x^3+4x^2-2x-x^3+6x^5
=6x^5-4x^3+29x^2-2x+2
b: bậc của P(x) là 5
c: hệ số lớn nhất là 6
Hệ số tự do là 2
P(-1)=-6+4+29+2+2=29+2=31
Đúng 0
Bình luận (0)
Tìm hệ số của \(x^4\) trong khai triển của biểu thức P = \(\left(1-x-3x^3\right)^n\) thành đa thức, biết n là số nguyên dương thoả mãn \(2\left(C^2_2+C^2_3+...+C^2_n\right)=3A^2_{n+1}\).
\(C_2^2+C_3^2+...+C_n^2=C_3^3+C_3^2+C_4^2+...+C_n^2\) (do \(C_2^2=C_3^3=1\))
\(=C_4^3+C_4^2+C_5^2+...+C_n^2=C_5^3+C_5^2+...+C_n^2\)
\(=...=C_n^3+C_n^2=C_{n+1}^3\)
Do đó:
\(2C_{n+1}^3=3A_{n+1}^2\Leftrightarrow\dfrac{2.\left(n+1\right)!}{3!.\left(n-2\right)!}=\dfrac{3.\left(n+1\right)!}{\left(n-1\right)!}\)
\(\Leftrightarrow n-1=9\Rightarrow n=10\)
\(\Rightarrow P=\left(1-x-3x^3\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(-x-3x^3\right)^k\)
\(=\sum\limits^{10}_{k=0}C_{10}^k\left(-1\right)^k\left(x+3x^3\right)^k=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^kx^i.3^{k-i}.x^{3\left(k-i\right)}\)
\(=\sum\limits^{10}_{k=0}\sum\limits^k_{i=0}C_{10}^kC_k^i\left(-1\right)^k.3^{k-i}.x^{3k-2i}\)
Ta có: \(\left\{{}\begin{matrix}0\le i\le k\le10\\i;k\in N\\3k-2i=4\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;2\right);\left(4;4\right)\)
Hệ số: \(C_{10}^2C_2^1\left(-1\right)^2.3^1+C_{10}^4C_4^4.\left(-1\right)^4.3^0=...\)
Đúng 1
Bình luận (1)

\(\Rightarrow he-so:\left[{}\begin{matrix}C^9_{10}C^1_9\left(-3\right)^{10-9}\left(-1\right)=270\\C^{10}_{10}C^4_{10}\left(-3\right)^{10-10}.\left(-1\right)^4=210\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho đa thức
\(A=3x^4+11x^3-7x^2-2x+1\)
hãy phân tích A thành 1 nhị thức bậc nhất và 1 đa thức bậc 3 có hệ số nguyên sao cho hệ số cao nhất của đa thức bậc 3 là 1