Trên đường cong y = 4 x 2 − 6 x + 3 , hãy tìm điểm tại đó tiếp tuyến song song với đường thẳng y = 2x.

Những câu hỏi liên quan
Cho đường cong (C) là đồ thị của hàm số y = x^2 - 4x + 3. Viết pt tiếp tuyến của đường cong đó. a) tại điểm Mo = (-2, 15) b) tại điểm có tung độ x = 3 c) k = 4
\(y'=2x-4\)
a.
\(y'\left(-2\right)=2.\left(-2\right)-4=-8\)
Phương trình tiếp tuyến:
\(y=-8\left(x+2\right)+15\Leftrightarrow y=-8x-1\)
b.
Gọi \(x_0\) là hoành độ tiếp điểm
\(\Rightarrow x_0^2-4x_0+3=3\Rightarrow x_0^2-4x_0=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=0\Rightarrow y'\left(0\right)=-4\\x_0=4\Rightarrow y'\left(4\right)=4\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=-4\left(x-0\right)+3\\y=4\left(x-4\right)+3\end{matrix}\right.\) \(\Leftrightarrow...\)
c.
Gọi \(x_0\) là hoành độ tiếp điểm \(\Rightarrow y'\left(x_0\right)=k=4\)
\(\Rightarrow2x_0-4=4\Rightarrow x_0=4\)
\(\Rightarrow y\left(4\right)=3\)
Pttt: \(y=4\left(x-4\right)+3\Leftrightarrow y=4x-13\)
Đúng 0
Bình luận (0)
tìm x < x cong 4/6> cong 3/4 - 1/2 =2 va 1/3
( x + 4/6 ) + 3/4 - 1/2 = 7/3
⇒ ( x + 4/6 ) + 1/4 = 7/3
⇒ x + 4/6 = 25/12
⇒ x = 17/12.
Vậy x = 17/12.
Đúng 0
Bình luận (0)
Cho hàm số y f(x) xác định, liên tục trên đoạn [-2;3] và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số y f(x) trên đoạn [-2; 3] A. 1 B. 0 C. 2. D. 3
Đọc tiếp
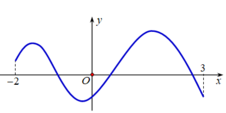
Cho hàm số y = f(x) xác định, liên tục trên đoạn [-2;3] và có đồ thị là đường cong trong hình vẽ bên. Tìm số điểm cực đại của hàm số y = f(x) trên đoạn [-2; 3]
A. 1
B. 0
C. 2.
D. 3
Đáp án C.
Quan sát đồ thị hàm số, ta thấy có hai điểm cực đại thuộc đoạn [-2; 3]
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho hai đường thẳng (d1): y = 3 - m(x - 2) và (d2): y = (-m + 1)x - 3. Quỹ tích giao điểm M của (d1) và (d2) là?
A. Một điểm nằm trên trục hoành.
B. Một điểm nằm trên trục tung.
C. Một đường thẳng.
D. Một đường cong dạng (P).
Giải thích.
Cho hàm số y - {x^2} + 2x + 3.a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là - 1,0,1,2,3 rồi vẽ chúng trong mặt phẳng tọa độ Oxy.b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số y - {x^2} + 2x + 3 (Hình 12).c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Đọc tiếp
Cho hàm số \(y = - {x^2} + 2x + 3\).
a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là \( - 1,0,1,2,3\) rồi vẽ chúng trong mặt phẳng tọa độ Oxy.
b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số \(y = - {x^2} + 2x + 3\) (Hình 12).
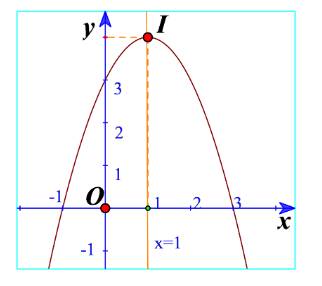
c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
a) \(x=-1\Rightarrow y=0\\ x=0\Rightarrow y=3\\ x=1\Rightarrow y=4\\ x=2\Rightarrow y=3\\ x=3\Rightarrow y=0\)
Lần lượt là: A(-1;0), B(0;3), I(1;4), C(2;3), D(3;0)
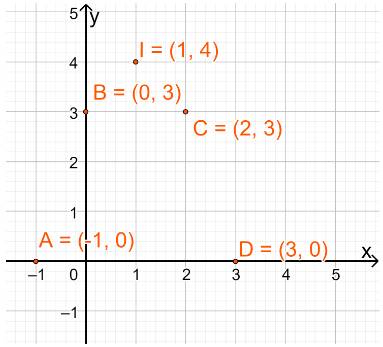
b) Vẽ đồ thị:
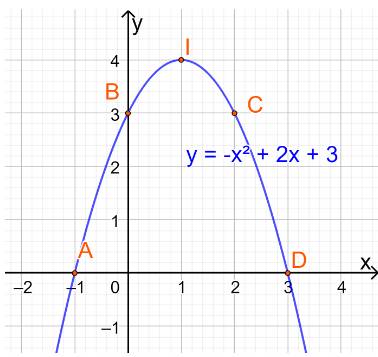
c) Điểm cao nhất là điểm I(1;4)
Phương trình trục đối xứng là đường thẳng x=1.
Đồ thị hàm số đó quay bề lõm xuống dưới.
Đúng 0
Bình luận (0)
Bài 1: Viết phương trình đồ thị hàm sốa) yx^3-3x^2+2 tại điểm (-1;-2)b) ydfrac{x^2+4x+5}{x+2} tại điểm có hoành độ bằng 0Bài 2: Viết phương trình tiếp tuyến với:a) Đường cong (C): yx^3+x-3 tại điểm có hoành độ bằng -1b) Đường cong (C): yx^3-3x^2 tại điểm có tung độ bằng -4c) Đường cong (C): ydfrac{x-3}{2x+1} tại điểm có hoành độ bằng -1Bài 3: Viết phương trình tiếp tuyến với:a) Đường cong (C): ydfrac{1}{3}3x^3-2x^2+3x+1 biết tiếp tuyến song song đường thẳng ydfrac{-3}{4}xb) Đường cong (C): ydfr...
Đọc tiếp
Bài 1: Viết phương trình đồ thị hàm số
a) \(y=x^3-3x^2+2 \) tại điểm (-1;-2)
b) \(y=\dfrac{x^2+4x+5}{x+2}\) tại điểm có hoành độ bằng 0
Bài 2: Viết phương trình tiếp tuyến với:
a) Đường cong (C): \(y=x^3+x-3\) tại điểm có hoành độ bằng -1
b) Đường cong (C): \(y=x^3-3x^2\) tại điểm có tung độ bằng -4
c) Đường cong (C): \(y=\dfrac{x-3}{2x+1}\) tại điểm có hoành độ bằng -1
Bài 3: Viết phương trình tiếp tuyến với:
a) Đường cong (C): \(y=\dfrac{1}{3}3x^3-2x^2+3x+1\) biết tiếp tuyến song song đường thẳng \(y=\dfrac{-3}{4}x\)
b) Đường cong (C): \(y=\dfrac{x^2+3x+1}{-x-2}\) biết tiếp tuyến song song với đường thẳng 2x+y-5=0
Bài 4: Cho đường cong (C): \(y=\dfrac{x^2-2x+2}{x-1}\). Viết phương trình tiếp tuyến của (C) biết:
a) Tại điểm có hoành độ bằng 6
b) Song song với đường thẳng \(y=-3x+29\)
c) Vuông góc với đường thẳng \(y=\dfrac{1}{3}x+2\)
Bài 5: Cho hàm số \(y=\dfrac{3x-2}{x-1}\) (C). Viết phương trình tiếp tuyến của đồ thị hàm số (C) biết:
a) Tiếp tuyến đi qua A(2;0)
b) Tiếp tuyến tạo với trục hoành 1 góc 45°
Mình làm xong hết rồi nhưng mà không biết đúng hay không. Nhờ mọi người giải giúp mình để mình thử đối chiếu đáp án được không ạ?
cho điểm A (-4,-2) đường tròn (C) (x-3)^2+(y+4)^2=12 đường thẳng d x+y-6=0. M là điểm di động trên (C). Tìm GTLN,GTNN của đoạn MA
cho đường cong y = x2, đường thẳng y = (2m + 1)x - 2 (x khác 1/2)
tìm m để |x1| + |x2| = 4 và x1 = 9x2
Xét pt hoành độ giao điểm của y = x2 và y = (2m + 1)x - 2 (x \(\ne\) \(\dfrac{1}{2}\))
x2 = (2m + 1)x - 2
\(\Leftrightarrow\) x2 - (2m + 1)x + 2 = 0
\(\Delta\) = [-(2m + 1)]2 - 4.1.2 = 4m2 + 4m + 1 - 8 = 4m2 + 4m - 7
Vì pt có 2 nghiệm x1; x2 \(\Rightarrow\) \(\Delta\) \(\ge\) 0 \(\Leftrightarrow\) m + \(\dfrac{1}{2}\) \(\ge\) \(\pm\)\(\sqrt{2}\) \(\Leftrightarrow\) m \(\ge\) \(\pm\sqrt{2}-\dfrac{1}{2}\)
x1 = \(\dfrac{2m+1+\sqrt{4m^2+4m-7}}{2}\)
x2 = \(\dfrac{2m+1-\sqrt{4m^2+4m-7}}{2}\)
|x1| + |x2| = 4 \(\Leftrightarrow\) \(\dfrac{4m+2}{2}=\pm4\) \(\Leftrightarrow\) 2m + 1 = \(\pm4\) \(\Leftrightarrow\) \(\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=\dfrac{-5}{2}\left(KTM\right)\end{matrix}\right.\)
Vậy ...
x1 = 9x2 \(\Leftrightarrow\) x1 - 9x2 = 0 \(\Leftrightarrow\) x1 + x2 - 10x2 = 0 \(\Leftrightarrow\) 4 - 10x2 = 0
\(\Leftrightarrow\) 10x2 = 4 \(\Leftrightarrow\) x2 = \(\dfrac{2}{5}\) \(\Leftrightarrow\) \(\dfrac{2m+1-\sqrt{4m^2+4m-7}}{2}=\dfrac{2}{5}\)
\(\Leftrightarrow\) 10m + 5 - 5\(\sqrt{4m^2+4m-7}\) = 4
\(\Leftrightarrow\) 1 + 10m = 5\(\sqrt{4m^2+4m-7}\)
\(\Leftrightarrow\) 1 + 20m + 100m2 = 25(4m2 + 4m - 7)
\(\Leftrightarrow\) 1 + 20m + 100m2 - 100m2 - 100m + 175 = 0
\(\Leftrightarrow\) -180m + 176 = 0
\(\Leftrightarrow\) m = \(\dfrac{44}{45}\) (TM)
Chúc bn học tốt! (Phần x1 = 9x2 ko chắc lắm)
Đúng 0
Bình luận (0)
Cho hàm số y f(x) có đạo hàm liên tục trên R và f(1) 1; f(-1) -1/3 Đặt
g
(
x
)
f
2
(
x
)
-
4
f
(
x
)
. Đồ thị của hàm số là đường cong ở hình bên. Mệnh đề nào sau đây đúng? A. B. C. D.
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên R và f(1) = 1; f(-1) = -1/3 Đặt
g
(
x
)
=
f
2
(
x
)
-
4
f
(
x
)
. Đồ thị của hàm số ![]() là đường cong ở hình bên. Mệnh đề nào sau đây đúng?
là đường cong ở hình bên. Mệnh đề nào sau đây đúng?
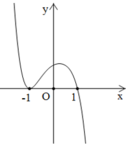
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
![]()
Từ đồ thị trên của ![]() suy ra BBT của
suy ra BBT của ![]() .
.
Suy ra ![]()
Do đó ![]()
![]() hoặc
hoặc ![]() .
.
Lập bảng biến thiên suy ra ![]()
Đúng 0
Bình luận (0)
Diện tích hình phẳng giới hạn bởi đường thẳng y=x+3 , đường cong y=x^2+1 là
Phương trình hoành độ giao điểm:
\(x^2+1=x+3\Leftrightarrow x^2-x-2=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
\(S=\int\limits^2_{-1}\left|x^2-x-2\right|dx=\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{1}{3}x^3+\dfrac{1}{2}x^2+2x\right)|^2_{-1}=\dfrac{9}{2}\)
Đúng 1
Bình luận (0)


















