Biểu diễn a b ở dạng tích các căn bậc hai với a < 0 và b < 0.

Những câu hỏi liên quan
Biểu diễn \(\sqrt{ab}\) ở dạng tích các căn bậc hai với a<0 và b<0
Áp dụng tính \(\sqrt{\left(-25\right).\left(-64\right)}\)
\(\sqrt{ab}=\sqrt{-a}.\sqrt{-b}\) (vì a<0 , b<0)
Áp dụng : \(\sqrt{\left(-25\right).\left(-64\right)}=\sqrt{-\left(-25\right)}.\sqrt{-\left(-64\right)}=\sqrt{25}.\sqrt{64}=5.8=40\)
Đúng 0
Bình luận (0)
Biểu diễn \(\sqrt{ab}\) ở dạng tích các căn bậc hai với \(a< 0;b< 0\)
Áp dụng tính \(\sqrt{\left(-25\right)\left(-64\right)}\)
Do a và b âm nên -a và -b dương
Khi đó , ta có: \(\sqrt{a.b}=\sqrt{\left(-a\right)\left(-b\right)}=\sqrt{-a}.\sqrt{-b}\)
Áp dụng , ta có: \(\sqrt{\left(-25\right)\left(-64\right)}=\sqrt{25}.\sqrt{64}=5.8=40\)
Đúng 0
Bình luận (0)
Biểu diễn a b với a < 0, b < 0 ở dạng thương của hai căn thức. Áp dụng tính - 49 - 81
Ta có: a < 0 nên -a > 0; b < 0 nên -b > 0
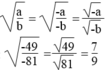
Đúng 0
Bình luận (0)
biểu diễn dưới dạng thương 2 căn bậc hai
a, \(\sqrt{\dfrac{3a}{b}}\left(a< 0,b< 0\right)\)
b, \(\sqrt{\dfrac{a}{xy}\left(a< 0,x< 0,y>0\right)}\)
a: \(=\sqrt{3a}:\sqrt{b}\)
b: \(=\sqrt{a}:\sqrt{xy}\)
Đúng 0
Bình luận (0)
Biểu diễn \(\sqrt{\frac{a}{b}}\) với a<0 và b<0 ở dạng thương của hai căn thức.Áp dụng tính \(\sqrt{\frac{-49}{-81}}\)
Với \(\begin{cases}a< 0\\b< 0\end{cases}\) thì \(\sqrt{\frac{a}{b}}=\sqrt{-a}:\sqrt{-b}\)
Áp dụng \(\sqrt{\frac{-49}{-81}}=\sqrt{-\left(-49\right)}:\sqrt{-\left(-81\right)}=\sqrt{49}:\sqrt{81}=7:9=\frac{7}{9}\)
Đúng 0
Bình luận (0)
Biểu diễn \(\sqrt{\dfrac{a}{b}}\) với \(a< 0;b< 0\) ở dạng thương của hai căn thức
Áp dụng tính \(\sqrt{\dfrac{-49}{-81}}\)
\(\sqrt{\dfrac{a}{b}}\)=\(\dfrac{\sqrt{a}}{\sqrt{b}}\) với a,b<0
Ta có : \(\sqrt{\dfrac{-49}{-81}}\)=\(\sqrt{\dfrac{49}{81}}\)=\(\dfrac{7}{9}\)
Đúng 0
Bình luận (0)
Biết a, b > 0 (a, b, c thuộc R)
Thì a>b khi <=> căn bậc hai của a > căn bậc hai của b
a>b <=> a^2 > b^2
Hãy so sánh:
a) 3 căn bậc hai của 2 và 2 căn bậc hai của 3
b) 7 căn bậc hai của 6 và 6 căn bậc 2 của 7
Giúp Minhg với mình tích choa!!!!!
(mk cần gấp)
cho a>0;b>0.so sánh căn bậc hai của a + căn bậc hai của b và căn bậc hai của a+b
Ai giải đúng và nhanh nhất tôi sẽ tick
bài 1:Cho các biểu thức sau:Asqrt{frac{2x+3}{x-3}} à Bfrac{sqrt{2x+3}}{sqrt{x-3}}a) Tìm x để A có nghãi.Tìm x để B có nghĩab) Với giá trị nào của x thì ABbài 2:Biểu diễn sqrt{frac{a}{b}} với a0 và b0 ở dạng thương của hai căn thứcÁp dụng tính: sqrt{frac{-49}{-81}}
Đọc tiếp
bài 1:Cho các biểu thức sau:
A=\(\sqrt{\frac{2x+3}{x-3}}\) à B=\(\frac{\sqrt{2x+3}}{\sqrt{x-3}}\)
a) Tìm x để A có nghãi.Tìm x để B có nghĩa
b) Với giá trị nào của x thì A=B
bài 2:Biểu diễn \(\sqrt{\frac{a}{b}}\) với a<0 và b<0 ở dạng thương của hai căn thức
Áp dụng tính: \(\sqrt{\frac{-49}{-81}}\)
Bài 1:
a) Để A,B có nghĩa \(\Leftrightarrow\begin{cases}2x+3\ge0\\x-3>0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-\frac{3}{2}\\x>3\end{cases}\)\(\Leftrightarrow x>3\)
b) Để A= B
\(\Leftrightarrow\sqrt{\frac{2x+3}{x-3}}=\frac{\sqrt{2x+3}}{\sqrt{x-3}}\)
\(\Leftrightarrow\sqrt{\frac{2x+3}{x-3}}-\sqrt{\frac{2x+3}{x-3}}=0\)
\(\Leftrightarrow0x=0\) (thỏa mãn với mọi x>3)
Vậy x>3 thì A=B
Đúng 0
Bình luận (1)
a, ĐKXĐ A: \(\frac{2x+3}{x-3}\)\(\frac{2x+3}{x-3}\ge0\Rightarrow\left[\begin{array}{nghiempt}\hept{\begin{cases}2x+3\ge0\\x-3>0\end{array}\right.\\\hept{\begin{cases}2x-3\le0\\x-3< 0\end{array}\right.\end{cases}\Rightarrow\left[\begin{array}{nghiempt}\hept{\begin{cases}x\ge-\frac{3}{2}\\x>3\end{array}\right.\\\hept{\begin{cases}x\le-\frac{3}{2}\\x< 3\end{array}\right.\end{cases}\Rightarrow}\left[\begin{array}{nghiempt}x>-\frac{3}{2}\\x< 3\end{array}\right.}\)
ĐKXĐ B: \(\begin{cases}2x+3\ge0\\x-3>0\end{cases}\Rightarrow\begin{cases}x\ge-\frac{3}{3}\\x>3\end{cases}}\)
Đúng 0
Bình luận (0)















