Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động. Tính xác suất để trong 3 học sinh được chọn có ít nhất một học sinh nữ
A. 2 3
B. 17 48
C. 17 24
D. 4 9
Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động. Tính xác suất để trong 3 học sinh được chọn có ít nhất một học sinh nữ.
A. 2 3 .
B. 17 48 .
C. 17 24 .
D. 4 9 .
Đáp án C.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản
Lời giải:
Chọn 3 học sinh trong 10 học sinh có C 10 3 cách => n ( Ω ) = C 10 3 = 120 .
Gọi X là biến cố trong 3 học sinh được chọn có ít nhất một học sinh nữ
Ta xét các trường hợp sau:
TH1. Chọn 1 học sinh nữ và 2 học sinh nam => có C 7 2 . C 3 1 = 63 cách.
TH2. Chọn 2 học sinh nữ và 1 học sinh nam => có C 7 1 . C 3 2 = 21 cách.
TH3. Chọn 3 học sinh nữ và 0 học sinh nam => có C 3 3 = 1 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 63 + 21 + 1 = 85.
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 85 120 = 17 24 .
Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đi tham gia chương trình áo ấm vùng cao. Tính xác suất để 3 học sinh được chọn có ít nhất một học sinh nữ.
`n(\Omega)=C_10 ^3`
Gọi `\overline A:"` Chọn `3` h/s mà trong đó không có h/s nữ`."`
`=>n(\overline A)=C_7 ^3`
`=>P(A)=1-[C_7 ^3]/[C_10 ^3]=17/24`
Một tổ có 12 học sinh gồm có 7 học sinh nam và 5 học sinh nữ, trong đó An là tổ trưởng còn Hoa là tổ phó. Chọn ngẫu nhiên 5 học sinh trong tổ để tham gia hoạt động tập thể của trường nhân dịp ngày thành lập Đoàn 26 tháng 3. Tính xác suất để sao cho nhóm học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai (An là học sinh nam, Hoa là học sinh nữ).
A. 0,24.
B.0.96.
C. 170/792
D.tất cả sai.
Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có ![]() cách.
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có ![]() cách.
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 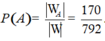
Chọn C.
từ một nhóm gồm 6 học sinh nữ và 4 học sinh nam, chọn ngẫu nhiên 3 học sinh. tính xác suất để chọn được 2 học sinh nữ và 1 học sinh nam
Không gian mẫu: \(C_{10}^3\)
Số cách chọn sao cho có 2 nữ 1 nam là: \(C_6^2.C_4^1\)
Xác suất: \(P=\dfrac{C_6^2.C_4^1}{C_{10}^3}=\dfrac{1}{2}\)
Lớp 10X có 25 học sinh, chia lớp 10X thành hai nhóm A và B sao cho mỗi nhóm đều có học sinh nam và học sinh nữ. Chọn ngẫu nhiên hai học sinh từ hai nhóm, mỗi nhóm một học sinh. Tính xác suất để chọn được hai học sinh nữ. Biết rằng, trong nhóm A có đúng 9 học sinh nam và xác suất chọn được hai học sinh nam bằng 0,54
A. 0,04
B. 0,08
C. 0,23
D. 0,46
Chọn A
Lời giải. Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * )
Suy ra số học sinh nữ trong nhóm B là
25 - 9 - x - y = 16 - x - y
Khi đó, nhóm A có: 9 nam, x nữ và nhóm B có
y nam, 16 - x - y nữ
Xác suất để chọn được hai học sinh nam là
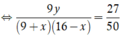
![]()
![]()
![]()
Mặt khác x + y < 16
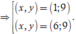
Vậy xác suất để chọn đươc hai học sinh nữ là
C 1 1 . C 6 1 C 10 1 . C 15 1 = 0 , 04
Lớp 10X có 25 học sinh, chia lớp 10X thành hai nhóm A và B sao cho mỗi nhóm đều có học sinh nam và học sinh nữ. Chọn ngẫu nhiên hai học sinh từ hai nhóm, mỗi nhóm một học sinh. Tính xác suất để chọn được hai học sinh nữ. Biết rằng, trong nhóm A có đúng 9 học sinh nam và xác suất chọn được hai học sinh nam bằng 0,54.
A. 0,42.
B. 0,04.
C. 0,46.
D. 0,23.
Đáp án B
Gọi số học sinh nữ trong nhóm A là x ( x ∈ ℕ * )
Gọi số học sinh nam trong nhóm B là y ( y ∈ ℕ * ) .
=> Số học sinh nữ trong nhóm B là 25 – 9 – x = 16 – x – y => x + y < 16
Khi đó, Nhóm A: 9 nam, x nữ và nhóm B: y nam, 16 – x – y nữ.
Xác suất để chọn được hai học sinh nam là
C 9 1 . C y 1 C 9 + x 1 . C 25 - 9 - x 1 = 0 , 54
⇔ 9 y ( 9 + x ) ( 16 - x ) = 27 50 .
⇒ y = 30 50 ( 9 + x ) ( 16 - x ) ⇒ x < 16 .
Vì y ∈ ℕ * ⇒ 3 50 ( 9 + x ) ( 16 - x ) ∈ N * .
=> (x, y) = {(1; 9), (6; 9), (11; 6)}.
Mặt khác x + y < 16
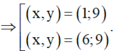
( Khi chia nhóm thì A,B có vai trò như nhau nên có 2 cặp thỏa mãn )
Vậy xác suất để chọn đươc hai học sinh nữ là 0,04.
Một tổ có 9 học sinh gồm 4 học sinh nữ và 5 học sinh nam. Chọn ngẫu nhiên từ tổ đó ra 3 hoc sinh. Xác suất để trong 3 học sinh chọn ra có số học sinh nam nhiều hơn số học sinh nữ bằng
A. 17 42 .
B. 5 42 .
C. 25 42 .
D. 10 42 .
Đáp án C.
Phương pháp:
Xác suất của biến cố A:
P A = n A n Ω .
Cách giải:
Số phần tử của không gian mẫu:
n Ω = C 9 3
A: “Số học sinh nam nhiều hơn số học sinh nữ”
Ta có 2 trường hợp:
+) Chọn ra 2 nam, 1 nữ:
+) Chọn ra 3 nam, 0 nữ.
⇒ n A = C 5 2 C 4 1 + C 5 3
⇒ P A = n A n Ω = C 5 2 C 4 1 + C 5 3 C 9 3 = 25 42
Một lớp học có 33 học sinh, trong đó có 10 học sinh giỏi, 11 học sinh khá và 12 học sinh trung bình. Chọn ngẫu nhiên trong lớp học 4 học sinh đi tham dự trại hè. Tính xác suất để nhóm học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình.
Gọi A là biến cố : "4 học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình"
Số phần tử không gian mẫu \(\left|\Omega\right|=C^4_{33}=40920\)
Ta có các trường hợp được chọn sau :
(1) Có 2 học sinh giỏi, 1 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^2_{10}.C^1_{11}.C^1_{12}=5940\).
(2)Có 1 học sinh giỏi, 2 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^2_{11}.C^1_{12}=6600\).
(3)Có 1 học sinh giỏi, 1 học sinh khá và 2 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^1_{11}.C^2_{12}=7260\).
Ta được \(\left|\Omega_A\right|=5940+6600+7260=19800\)
Do đó : \(P\left(A\right)=\frac{\left|\Omega_A\right|}{\left|\Omega\right|}=\frac{15}{31}\)
Trong nhóm 60 học sinh có 30 học sinh thích học Toán, 25 học sinh thích học Lý và 10 học sinh thích cả Toán và Lý. Chọn ngẫu nhiên 1 học sinh từ nhóm này. Xác suất để được học sinh này thích học ít nhất là một môn Toán hoặc Lý?
A. 4/5
B. 3/4
C. 2/3
D. 1/2
Gọi B là tập hợp “học sinh thích học Lý”
Gọi C là tập hợp ” học sinh thích học ít nhất một môn “
Ta có n(C) = n( A ∪ B) = n(A) + n(B) – n(A ∩ B) = 30 + 25 – 10 = 45
Vậy xác suất để được học sinh này thích học ít nhất là một môn Toán hoặc Lý là: 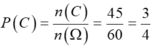
Chọn B.