Cho hàm số y = x 2 - 2 x + 4 có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 0 là
A. y = 4x + 3
B. y = 1 2 x + 2
C. y = - 1 2 x + 2
D. y = - 1 2 x - 2
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
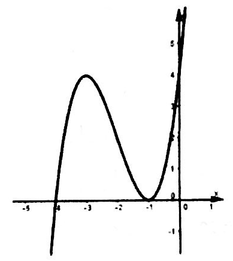
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Cho hàm số y=f(x)=(a-1)x+3 tìm a để
a. Đồ thị hàm số cắt đường thẳng y=-x+10
b. Đồ thị hàm số cắt rrucj hoành tại điểm có hoàng độ x=4
c. Đồ thị hàm số cắt trục tung tại điểm có tung độ y=2
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y=f(x)=2/3.x
a) Tìm f(7); f(-5/4)
b)Tìm x khi y=10
c)Tìm x khi f(x)=8
d)Vẽ đồ thị hàm số trên.
e) Hỏi điểm P(9;16) có thuộc đồ thị hàm số y=2/3 x ko?
g) Tìm điểm K và H trên đồ thị hàm số y=2/3x biết xK =6,yH =4.
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Đáp án C
Phương pháp : Xác định hàm số f’(x) từ đó tính được ![]()
Cách giải : Ta dễ dàng tìm được phương trình parabol là
![]()
![]()
Đồ thị hàm số đi qua gốc tọa độ ![]()
![]()
Cho hàm số bậc nhất y=(m+1)x-2 có đồ thị là đường thẳng (d).
a)Tìm m để đồ thị hàm số (d) cắt đồ thị hàm số y=x+4 tại điểm có hoành độ là :-2.
b)Vẽ đồ thị hàm số vừa tìm được ở câu a).
c)Tính diện tích tam giác tạo bởi đồ thị hàm số (d)với hai trục tọa độ.(giúp mình ,cảm ơn)
a, Thay x = -2 => y = -2 + 4 = 2 => A(-2;2)
(d) cắt y = x + 4 tại A(-2;2) <=> 2 = -2 ( m + 1 ) - 2
<=> -2m - 2 - 2 = 2 <=> -2m = 6 <=> m = -3
Vậy (d) : y = -2x - 2
b, bạn tự vẽ nhé
c, Cho x = 0 => y = -2
=> (d) cắt trục Oy tại A(0;-2) => OA = | -2 | = 2
Cho y = 0 => x = -1
=> (d) cắt trục Ox tại B(-1;0) => OB = | -1 | = 1
Ta có : \(S_{OAB}=\frac{1}{2}.OA.OB=\frac{1}{2}.2.1=1\)( dvdt )
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\hept{m+5=22m−10≠−1\hept{m+5=22m−10≠−1 <=> \hept{m=−3m≠92\hept{m=−3m≠92 <=> m=−3
Giả sử (d) luôn đi qua điểm cố định M(x0; y0)
Ta có: y0=(m+5)x0+2m−10y0=(m+5)x0+2m−10
<=> mx0+5x0+2m−10−y0=0mx0+5x0+2m−10−y0=0
<=> m(xo+2)+5x0−y0−10=0m(xo+2)+5x0−y0−10=0
Để M cố định thì: \hept{x0+2=05x0−y0−10=0\hept{x0+2=05x0−y0−10=0 <=> \hept{x0=−2y0=−20\hept{x0=−2y0=−20
Vậy...
????????????????
Cho hàm số y=f(x)=3X
a, Vẽ đồ thị hàm số
b, Tính f(5); f(-7/12)
c, Các điểm M( -2:6), C( 4/9; 4/3) có thuộc đồ thị hàm số không ? Vì sao
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm và đồ thị hàm số y= f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
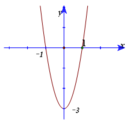
A. y =x3-3x+2.
B. y=x3+3x+2.
C. y=x3-2x+2.
D. y =x3-3x-1.
+ Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’( x), ta thấy đồ thị hàm số y= f’ (x) là parabol có trục đối xứng là trục tung nên b=0
Đồ thị hàm số y= f’( x) đi qua 2 điểm (1;0) và (0; -3) thay vào f’(x) ; ta tìm được: a=1 và c= -3.
Suy ra: f’(x) = 3x2-3b và f(x) = x3-3x+d.
+ Do (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm nên ta có:
f’(x) =0 khi và chỉ khi x= -1;x= 1( loại)
Như vậy (C) đi qua điểm (-1; 4) ta tìm được d= 2
Khi đó; f( x) =x3-3x+2.
chọn A.
Cho hàm số \(y=x^4-2x^2\) có đồ thị (C) . Hỏi có bao nhiêu tiếp tuyến của đồ thị (C) song song với trục hoành ?
Lời giải:
Để PTTT tại $x=x_0$ song song với trục hoành thì $f'(x_0)=0$ và $f(x_0)\neq 0$
$f'(x)=4x^3-4x=0\Leftrightarrow x=0;1;-1$
Thử các giá trị $x$ này vô $f(x_0)$ xem có khác $0$ hay không ta thu được $x=\pm 1$
Tức là có 2 tiếp tuyến của $(C)$ song song với trục hoành.