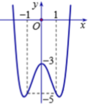
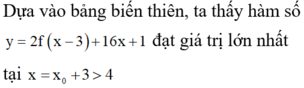Đồ thị sau đây của hàm số y = x 4 - 3 x 2 - 3 . Với giá trị nào của m thì phương trình x 4 - 3 x 2 + m = 0 có ba nghiệm phân biệt?
A.m=-4
B.m=0
C.m=-3
D.m=4
Bài 1.cho hàm số y= 4/5.x
a)vẽ đồ thị hàm số
b)tìm giá trị của hàm số tại x=(-1);x=0
bài 2. cho hàm số y=-2/5.x
a)vẽ đồ thị hàm số
b)trong các điểm sau đây thì điểm nào thuộc đồ thị hàm số đó:M(-5;2);N(0;3);P(3;hỗn số -1,1/5)
Tìm khẳng định đúng trong các khẳng định sau đây:
A. Hàm số y = x 3 - 5 có hai cực trị;
B. Hàm số y = x 4 /4 + 3 x 2 - 5 luôn đồng biến;
C. Tiệm cận ngang của đồ thị hàm số y = 3 x - 2 5 - x là y = -3;
D. Đồ thị hàm số sau có hai tiệm cận đứng
y
=
3
x
2
-
2
x
+
5
x
2
+
x
+
7
Đáp án: C.
y = -3 là tiệm cận ngang của đồ thị hàm số
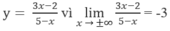
a) Vẽ đồ thị của hàm số: \(y = 0,5x;y = - 3x;y = x\).
b) Các đồ thị sau đây là đồ thị của hàm số nào?
a)
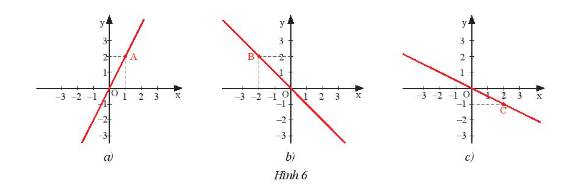
- Vẽ đồ thị hàm số \(y = 0,5x\)
Cho \(x = 1 \Rightarrow y = 0,5.1 = 0,5\). Ta vẽ điểm \(A\left( {1;0,5} \right)\)
Đồ thị hàm số \(y = 0,5x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;0,5} \right)\).
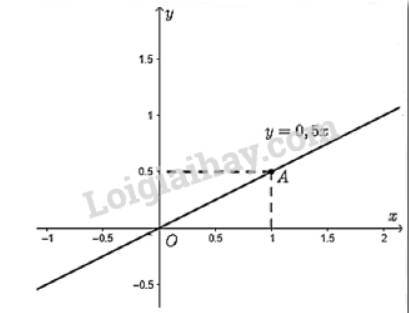
- Vẽ đồ thị hàm số \(y = - 3x\)
Cho \(x = 1 \Rightarrow y = - 3.1 = - 3\). Ta vẽ điểm \(B\left( {1; - 3} \right)\)
Đồ thị hàm số \(y = - 3x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(B\left( {1; - 3} \right)\).
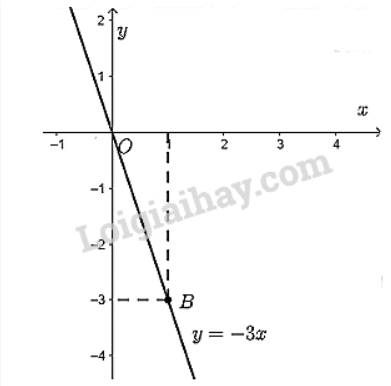
- Vẽ đồ thị hàm số \(y = x\)
Cho \(x = 1 \Rightarrow y = 1\). Ta vẽ điểm \(C\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(C\left( {1;1} \right)\).
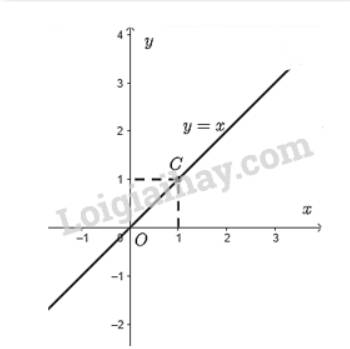
b) Ta thấy cả ba đồ thị đều đi qua gốc tọa độ \(O\left( {0;0} \right)\) nên có dạng \(y = ax\).
- Ở đồ thị a, đồ thị hàm số đi qua điểm \(A\left( {1;2} \right)\) nên ta có: \(2 = a.1 \Rightarrow a = 2\).
Do đó, đồ thị a là đồ thị của hàm số \(y = 2x\).
- Ở đồ thị b, đồ thị hàm số đi qua điểm \(B\left( { - 2;2} \right)\) nên ta có: \(2 = a.\left( { - 2} \right) \Rightarrow a = 2:\left( { - 2} \right) = - 1\).
Do đó, đồ thị b là đồ thị của hàm số \(y = - x\).
- Ở đồ thị c, đồ thị hàm số đi qua điểm \(C\left( {2; - 1} \right)\) nên ta có: \( - 1 = a.2 \Rightarrow a = \left( { - 1} \right):2 = \dfrac{{ - 1}}{2}\).
Do đó, đồ thị b là đồ thị của hàm số \(y = \dfrac{{ - 1}}{2}x\).
Cho hàm số y=1,5x
a) Vẽ đồ thị hàm số y=1,5 x
b) điểm nào sau đây thuộc đồ thị của hàm số trên: M( -2:3); N( 3;6)
a) y = 1,5x
Với x = 2 thì y = 1,5 . 2 = 3
Ta có: A (2; 3)
Vậy đồ thị hàm số y = 1,5x là một đường thẳng đi qua 2 điểm O (0; 0) và A (2; 3)
(Vẽ hình hơi xấu 1 chút, thông cảm ![]() )
)
b) *Xét M (-2; 3)
Với x = -2 thì y = 1,5 . (-2) = -3 (bằng tung độ điểm M)
Vậy điểm M thuộc đồ thị hàm số y = 1,5x
*Xét điểm N (3; 6)
Với x = 3 thì y = 1,5 . 3 = 4,5 (không bằng tung độ điểm N)
Vậy điểm N không thuộc đồ thị hàm số y = 1,5x
Mọi người giúp mk câu này vs ạ
Bài 8. Cho hàm số y = f(x) = x -2
a)Tính f(-1) ; f(0)
b)Tìm x để f(x) = 3
c)Điểm nào sau đây thuộc đồ thị của hàm số y = f(x) = x -2 : A(1;0) ; B(-1;-3) C(3;-1)
Bài 9. a) Vẽ đồ thị của hàm số y = - 2x
b) Điểm sau điểm nào thuộc đồ thị hàm số: A (-2; 4); B(-1; -2)
Bài 10: Cho hàm số y = f(x) = ax (a # 0)
a)Tìm a biết đồ thị hàm số đi qua điểm A( 1; -3)
b)Vẽ đồ thị ứng với giá trị a vừa tìm được
Bài 8:
a) f(-1) = (-1) - 2 = -3
f(0) = 0 - 2 = -2
b) f(x) = 3
\(\Rightarrow x-2=3\)
\(x=3+2\)
\(x=5\)
Vậy \(x=5\) thì f(x) = 3
c) Thay tọa độ điểm A(1; 0) vào hàm số, ta có:
VT = 0; VP = 1 - 2 = -1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm A(1; 0) không thuộc đồ thị của hàm số đã cho
Thay tọa độ điểm B(-1; -3) vào hàm số, ta có:
VT = -3; VP = -1 - 2 = -3
\(\Rightarrow VT=VP=-3\)
\(\Rightarrow\) Điểm B(-1; -3) thuộc đồ thị hàm số đã cho
Thay tọa độ điểm C(3; -1) vào hàm số, ta có:
VT = -1; VP = 3 - 2 = 1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm C(3; -1) không thuộc đồ thị hàm số đã cho.
Bài 8:
a. y = f(x) = -1- 2= -3
y = f(x) = 0-2= -2
b. cho y = f(x)= 3
ta có: 3=x-2 => x-2=3
x= 3+2
x= 5
c. điểm B
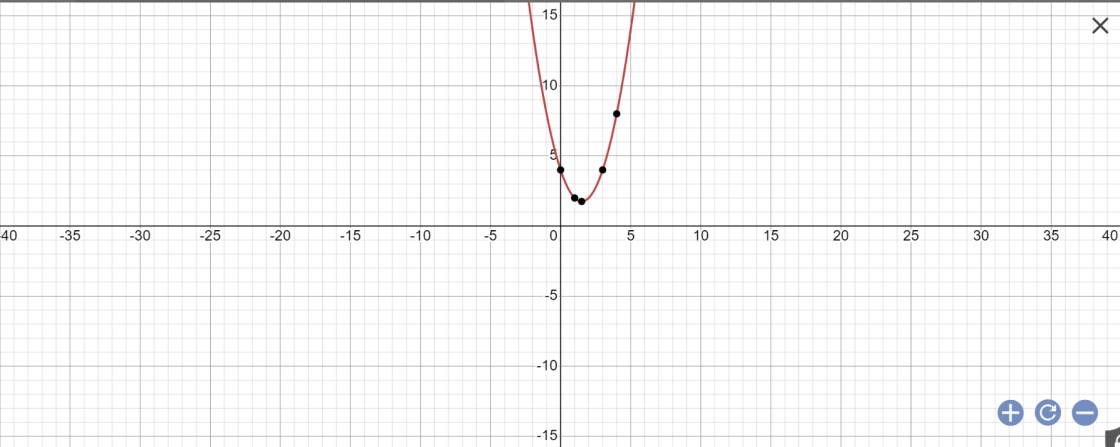
Vẽ đồ thị các hàm số sau đây a) y = x ^ 2 - 3x + 4 b) y = - x ^ 2 + 2x + 3 Giúp mk vs
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-\left(-3\right)}{2}=\dfrac{3}{2}\\y=-\dfrac{\left(-3\right)^2-4\cdot1\cdot4}{4\cdot1}=-\dfrac{9-16}{4}=\dfrac{7}{4}\end{matrix}\right.\)
Vì \(y=x^2-3x+4\) có a=1>0
nên hàm số sẽ đồng biến khi \(x>\dfrac{3}{2}\) và nghịch biến khi \(x< \dfrac{3}{2}\)
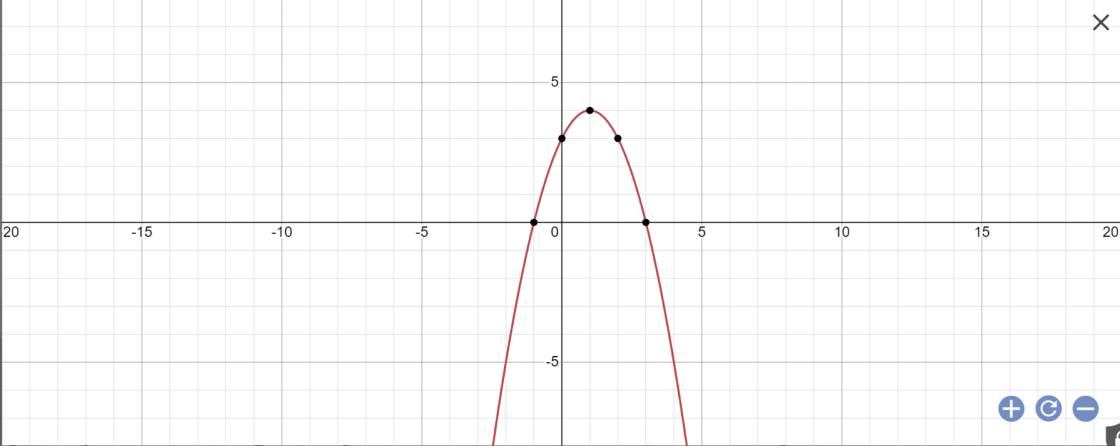
b: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=-\dfrac{2}{2\cdot\left(-1\right)}=\dfrac{-2}{-2}=1\\y=-\dfrac{2^2-4\cdot\left(-1\right)\cdot3}{4\cdot\left(-1\right)}=-\dfrac{4+12}{-4}=4\end{matrix}\right.\)
Vì \(y=-x^2+2x+3\) có a=-1<0
nên hàm số đồng biến khi x<1 và nghịch biến khi x>1
Vẽ đồ thị các hàm số sau đây và tìm giao điểm của chúng với các trục tọa độ.
A)y =x + 1 nếu x ≥ 2
4 − x nếu x ≤ 2
B) y = |2x − 3|
b: \(y=0\Leftrightarrow\left|2x-3\right|=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
\(x=0\Leftrightarrow y=3\)
Cho các hàm số bậc nhất: \(y = \dfrac{1}{3}x + 2\); \(y = - \dfrac{1}{3}x + 2\);\(y = - 3x + 2\). Kết luận nào sau đây đúng?
A. Đồ thị của các hàm số trên là các đường thẳng song song với nhau.
B. Đồ thị của các hàm số trên là các đường thẳng đi qua gốc tọa độ.
C. Đồ thị của các hàm số trên là các đường thẳng trùng nhau.
D. Đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.
Đáp án đúng là D
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) là đường thẳng có hệ số góc là \(a = - \dfrac{1}{3}\).
- Đồ thị hàm số \(y = - 3x + 2\) là đường thẳng có hệ số góc là \(a = - 3\).
Vì cả ba đường thẳng đều có hệ số góc khác nhau nên chúng cắt nhau.
- Đồ thị hàm số \(y = \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\).
- Đồ thị hàm số \(y = - \dfrac{1}{3}x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
- Đồ thị hàm số \(y = - 3x + 2\) cắt trục tung tại điểm \(A\left( {0;2} \right)\)
Do đó điểm \(A\left( {0;2} \right)\) là giao điểm của ba đồ thị hàm số.
Vậy đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
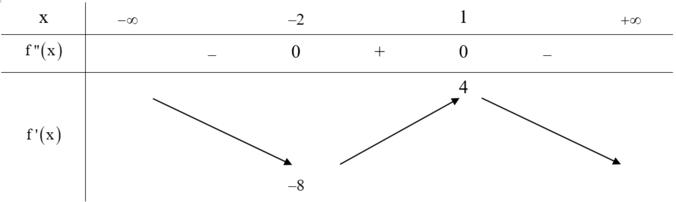
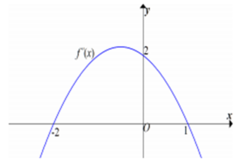
Cho hàm số y=f(x) có đạo hàm cấp hai liên tục trên ℝ . Biết f ' − 2 = − 8 , f ' 1 = 4 và đồ thị của hàm số f"(x) như hình vẽ dưới đây. Hàm số y = 2 f x − 3 + 16 x + 1 đạt giá trị lớn nhất tại x 0 thuộc khoảng nào sau đây?
A. 0 ; 4
B. 4 ; + ∞
C. − ∞ ; 1
D. − 2 ; 1
B
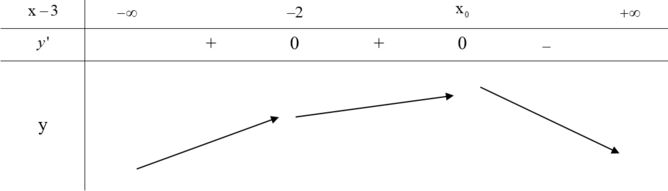
Từ đồ thị của hàm số f"(x) ta có bảng biến
thiên của hàm số f'(x) như sau: