Cho hàm số y = x − 2 x − 3 có đồ thị (C). Tìm m để đường thẳng d đi qua A ( 0 ; m ) có hệ góc bằng 2 cắt (C) tại 2 điểm phân biệt có hoành độ dương
A. m ∈ ℝ .
B. 2 3 < m < 7 .
C. m < 2 3 .
D. m > 7 .
Những câu hỏi liên quan
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y= 2+ x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = 2 - x, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x - 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
Cho hàm số y = x + 2, vẽ đồ thị hàm số của y khi x = -2,-1,0,1,2,3
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Đúng 0
Bình luận (0)
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Với các hàm số bậc nhất, hãy cho biết hàm số đó đồng biến hay nghịch biến? a)y=5-2x b)y=x√2-1. C)y=2(x+1)-2x. D)y=3(x-1)x. e)y=-2/3 x. f)y=x+ 1/x
Các hàm số a,b,e là các hàm số bậc nhất
Đúng 1
Bình luận (1)
Trong các hàm số sau,hàm số nào là hàm số bậc nhất ? Với các hàm số bậc nhất , hãy cho biết hàm số đó đồng biến hay nghịch biến ?
a) y = 5 - 2x b) y = x√2 -1 c) y = 2(x+1) - 2x
d) y = 3(x-1) - x e) y = -2/3x f) y= x + 1/x
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
Đúng 1
Bình luận (0)
Cho hàm số y f( x) có đạo hàm là hàm số y f’(x) trên R. Biết rằng hàm số y f’ ( x-2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y f( x) nghịch biến trên khoảng nào? A. . B. (- 1; 1) C. . D. .
Đọc tiếp
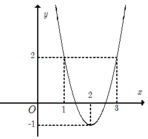
Cho hàm số y= f( x) có đạo hàm là hàm số y= f’(x) trên R. Biết rằng hàm số y= f’ ( x-2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y= f( x) nghịch biến trên khoảng nào?
A. 
.
B. (- 1; 1)
C. 
.
D. 
.
Bài 1: Xét tính đơn điệu của hàm số yf(x) khi biết đạo hàm của hàm số là:a) f(x)(x+1)(1-x^2)(2x-1)^3b) f(x)(x+2)(x-3)^2(x-4)^3Bài 2: Cho hàm số yf(x) có đạo hàm f(x)x(x+1)(x-2). Xét tính biến thiên của hàm số:a) yf(2-3x)b) yf(x^2+1)c) yf(3x+1)
Đọc tiếp
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Cho hàm số
y
f
(
x
)
có đạo hàm
f
(
x
)
x
(
x
-
1
)
2
(
x
-
2
)
. Tìm khoảng nghịch biến của đồ thị hàm số
y
f
(
x
)
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) 2 ( x - 2 ) . Tìm khoảng nghịch biến của đồ thị hàm số y = f ( x )
Cho hàm số yf(x) có đạo hàm
f
’
(
x
)
x
(
x
-
1
)
2
(
x
-
2
)
. Tìm khoảng nghịch biến của đồ thị hàm số yf(x) A. (∞;0) và (1;2) B. (0;1) C. (0;2) D. (2;+∞)
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ’ ( x ) = x ( x - 1 ) 2 ( x - 2 ) . Tìm khoảng nghịch biến của đồ thị hàm số y=f(x)
A. (∞;0) và (1;2)
B. (0;1)
C. (0;2)
D. (2;+∞)
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = x ( x - 1 ) ( x + 2 ) 3 ( x - 2 ) 2 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 4
B. 7
C. 3
D. 2
