Cho hàm số f ( x ) = 1 x 2 1 - x 2 Tìm nguyên hàm của hàm số g ( t ) = c o s t . f ( sin t ) , với t ∈ ( - π 2 ; π 2 ) ∖ { 0 } là
A. F(t)=-tant+C
B. F(t)=-cott+C
C. F(t)=tant+C
D. F(t)=cott+C
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
a) cho hàm số y=(f)x=x^6+1/x^3.cmr f(1/2)=f(x)
b) cho hàm số y=(f)x=x^2+1/x^2.CMR f(x)=f(-x)
c) cho hàm số y=(f)x=5^x. Tính f(x+1)-f(x)
HELPPPPPPPPPPPPP ME!
Bài 1: Cho hàm số y =f( x)= -5x -1. Tính f(-1), f(0), f(1), f(1/2)
Bài 2: a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f(-1/2); f(1/2).
b) Cho hàm số y = g(x) = x – 1. Tính g(-1); g(0) ; g(1) ; g(2).
c) Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Lm giúp mình vs mình đang cần gấp .
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Bài 2:
a: f(-2)=7
f(-1)=5
f(0)=3
CHO HÀM SỐ f(x)=x^2+6x-4. tìm f(x-1)
cho hàm số f(x+1/x)=x^2+1/x^2. tìm f(x)
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
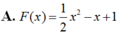
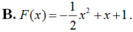
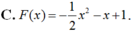
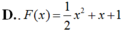
Bài 1. Cho hàm số y= f(x)= {-2(x2 + 1) khi x ≤ 1 Tính f(1);f(2),f(√2 phần 2);f(√2)
{4√x-1 khi x > 1
Bài 2.Cho hàm số y= f(x)= { √-3x+8 khi x < 2 Tính f(-3);f(2);f(1),f(9)
{√x+7 khi x ≥ 2
Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.
cho hàm số y=1/2x
a.vẽ đồ thị hàm số trên
b.tính f(2), f(1), f(-2), f(-1), f(0)
c.tính giá trị của x khi f(x)=2 ,f(x)=1, f(x)=-1
d.những điểm nào sau đây thuộc đồ thị hàm số A(-1,1/2) B(-1,-1/2)
a: 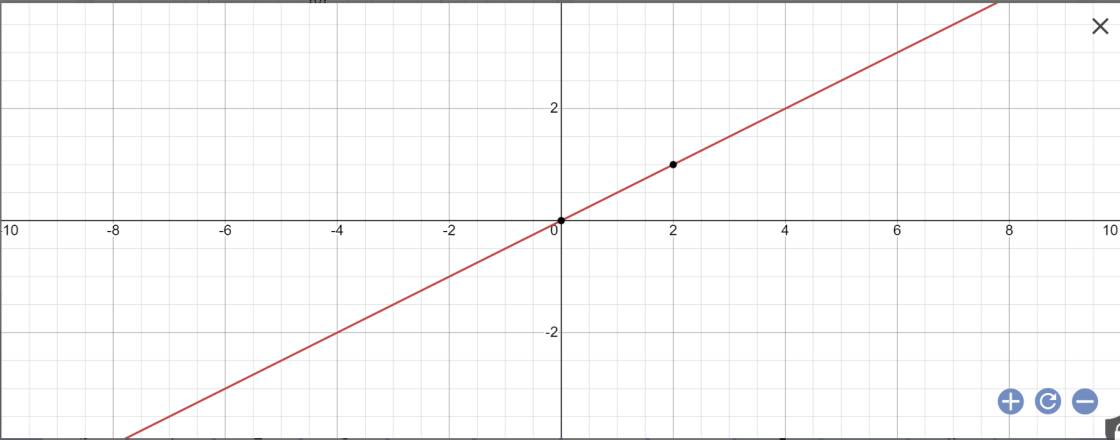
b: \(f\left(2\right)=\dfrac{1}{2}\cdot2=1\)
\(f\left(1\right)=\dfrac{1}{2}\cdot1=\dfrac{1}{2}\)
\(f\left(-2\right)=\dfrac{1}{2}\cdot\left(-2\right)=-1\)
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\)
\(f\left(0\right)=\dfrac{1}{2}\cdot0=0\)
c: f(x)=2
=>\(\dfrac{1}{2}x=2\)
=>x=2*2=4
f(x)=1
=>\(\dfrac{1}{2}x=1\)
=>\(x=1:\dfrac{1}{2}=2\)
f(x)=-1
=>\(\dfrac{1}{2}x=-1\)
=>\(x=-1\cdot2=-2\)
d: \(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\ne\dfrac{1}{2}=y_A\)
=>A(-1;1/2) không thuộc đồ thị hàm số y=1/2x
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}=y_B\)
=>\(B\left(-1;-\dfrac{1}{2}\right)\) thuộc đồ thị hàm số y=1/2x
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 2 ( x - 1 ) 3 ( 2 - x ) . Hàm số f ( x ) đồng biến trên khoảng nào dưới đây
![]()
![]()
![]()
Cho hàm số f(x) có đạo hàm f ’ ( x ) = x 2019 ( x - 1 ) 2 ( x + 1 ) 3 . Số điểm cực đại của hàm số f(x) là
A. 1
B. -1
C. 0
D. 3
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)