Sửa lại đề bài là \(cos\left(15^o+2\alpha\right)\) (chứ không phải là \(cos^2\left(15^o+2\alpha\right)\) nhé)

 Ta có \(VT=sin^2\left(45^o+\alpha\right)-sin^2\left(30^o-\alpha\right)-sin15^o.cos^2\left(15^o+2\alpha\right)\)

\(=\left[sin\left(45^o+\alpha\right)+sin\left(30^o-\alpha\right)\right]\left[sin\left(45^o+\alpha\right)-sin\left(30^o-\alpha\right)\right]-sin15^ocos^2\left(15^o+2\alpha\right)\)

\(=2sin\left(\dfrac{75^o}{2}\right)cos\left(\dfrac{2\alpha+15^o}{2}\right).2cos\left(\dfrac{75^o}{2}\right)sin\left(\dfrac{2\alpha+15^o}{2}\right)-sin15^ocos^2\left(15^o+2\alpha\right)\)

\(=sin75^o.sin\left(2\alpha+15^o\right)-sin15^o.cos^2\left(2\alpha+15^o\right)\)

\(=sin\left(2\alpha+15^o-15^o\right)\) (dùng \(sin\left(\alpha-\beta\right)=sin\alpha.cos\beta-sin\beta.cos\alpha\))

\(=sin2\alpha=VP\)

Vậy đẳng thức được chứng minh.

Mấy chỗ kia bạn sửa hết \(cos^2\left(15^o+2\alpha\right)\) thành \(cos\left(15^o+2\alpha\right)\) nhé.

a) sin²30 độ - sin²40 độ - sin²50 độ + sin² 60 độ

= cos²60^o - cos²50^o - sin²50^o + sin²60^o

= (cos²60^o + sin²60^o) - (cos²50^o + sin²50^o)

= 1 - 1 = 0

b) cos²25 độ - cos²35độ + cos²45 độ -cos² 55 độ + cos² 65 độ

= sin²65^o - sin²55^o + cos²45^o - cos²55^o + cos²65^o

= (sin²65^o + cos²65^o) - (sin²55^o + cos²55^o) + cos²45^o

=  1 - 1 +1/2

= 1/2

\(\dfrac{sin2\alpha+sin5\alpha-sin3\alpha}{1+cos\alpha-2sin^22\alpha}\)

\(=\dfrac{2cos\dfrac{5\alpha}{2}.sin\left(-\dfrac{\alpha}{2}\right)+2sin\dfrac{5\alpha}{2}.cos\dfrac{5\alpha}{2}}{cos4\alpha+cos\alpha}\)

\(=\dfrac{2cos\dfrac{5\alpha}{2}.\left(sin\dfrac{5\alpha}{2}-sin\dfrac{\alpha}{2}\right)}{2cos\dfrac{5\alpha}{2}.cos\dfrac{3\alpha}{2}}\)

\(=\dfrac{4cos\dfrac{5\alpha}{2}.cos\dfrac{3\alpha}{2}.sin\alpha}{2cos\dfrac{5\alpha}{2}.cos\dfrac{3\alpha}{2}}\)

\(=2sin\alpha\)

Sử dụng 2 công thức: \(sina=cos\left(90^0-a\right)\) và \(sin^2a+cos^2a=1\) ta có:

\(A=sin^25^0+cos^2\left(90^0-85^0\right)=sin^25^0+cos^25^0=1\)

Đáp án B

Theo giả thiết có 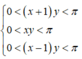 và

Và thay vào đẳng thức điều kiện có:

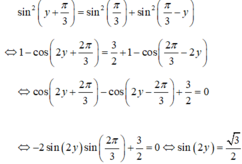
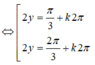
Đối chiếu với điều kiện nhận 

\(S_{HKE}=S_{ABC}-S_{AKE}-S_{BHE}-S_{CHK}\)

\(\Leftrightarrow\dfrac{S_{HKE}}{S_{ABC}}=1-\dfrac{S_{AKE}}{S_{ABC}}-\dfrac{S_{BHE}}{S_{ABC}}-\dfrac{S_{CHK}}{S_{ABC}}\)

\(\Leftrightarrow\dfrac{1}{4}=1-\dfrac{\dfrac{1}{2}AE.AK.sinA}{\dfrac{1}{2}AB.AC.sinA}-\dfrac{\dfrac{1}{2}BH.BE.sinB}{\dfrac{1}{2}AB.BC.sinB}-\dfrac{\dfrac{1}{2}CH.CK.sinC}{\dfrac{1}{2}AC.BC.sinC}\)

\(\Leftrightarrow\dfrac{AE.AK}{AB.AC}+\dfrac{BH.BE}{AB.BC}+\dfrac{CH.CK}{AC.BC}=\dfrac{3}{4}\)

(Để ý rằng \(\dfrac{AE}{AC}=cosA\) do tam giác ACE vuông tại E và tương tự...)

\(\Leftrightarrow cosA.cosA+cosB.cosB+cosC.cosC=\dfrac{3}{4}\)

\(\Leftrightarrow cos^2A+cos^2B+cos^2C=\dfrac{3}{4}\)

\(\Leftrightarrow1-sin^2A+1-sin^2B+1-sin^2C=\dfrac{3}{4}\)

\(\Leftrightarrow sin^2A+sin^2B+sin^2C=\dfrac{9}{4}\)

\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)

\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)

\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)