Biết ∫ π 4 π 3 1 cos 4 x + sin x co s 3 x d x = a - b + c ln 2 + d ln ( 1 + 3 ) với a,b,c,d là các số hữu tỉ. Giá trị của abcd bằng
A. 0
B. -36
C. -24
D. -6
Tính:F=Cos(π/4+α) x cos(π/4-α)
G=Sin(π/3+α) x cos(π/3-α)
H=cos(π/2-α) x sin(π/2+α)
I=sin(π/4+α) - cos(π/4-α)
K=cos(π/6-x) - sin(π/3+x)
Biết sinα = 3/4 và π/2 < α < π. Tính
![]()
Hai dao động điều hoà cùng phương, cùng tần số có phương trình lần lượt là : x 1 = 3cos(5 π t/2 + π /6)(cm) và x 2 = 3cos(5 π t/2 + 3 π /3)(cm). Biên độ và pha ban đầu của dao động tổng hợp là
A. 6 cm ; π /4 rad. B. 5,2 cm ; π /4 rad.
C. 5,2 cm ; π /3 rad. D. 5,8 cm ; π /4 rad.
Tìm x biết ba số cos(x-π/4); sinx; cos(x+π/4) là 3 số hạng liên tiếp của cấp số nhân
Để \(cos\left(x-\dfrac{\Omega}{4}\right);sinx;cos\left(x+\dfrac{\Omega}{4}\right)\) là ba số hạng liên tiếp của cấp số nhân thì \(sin^2x=cos\left(x-\dfrac{\Omega}{4}\right)\cdot cos\left(x+\dfrac{\Omega}{4}\right)\)
=>\(sin^2x=\sqrt{2}\left(cosx-sinx\right)\cdot\sqrt{2}\left(cosx+sinx\right)\)
=>\(sin^2x=2cos^2x-2sin^2x\)
=>\(3\cdot sin^2x=2\cdot cos^2x\)
=>\(\dfrac{sin^2x}{cos^2x}=\dfrac{2}{3}\)
=>\(tan^2x=\dfrac{2}{3}\)
=>\(\left[{}\begin{matrix}tanx=\dfrac{\sqrt{6}}{3}\\tanx=-\dfrac{\sqrt{6}}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=arctan\left(\dfrac{\sqrt{6}}{3}\right)+k\Omega\\x=arctan\left(-\dfrac{\sqrt{6}}{3}\right)+k\Omega\end{matrix}\right.\)
Tìm GTLN GTNN
y = 2cos22x + 2cos2x - 4
y = tan2x - 2√3 tanx -1 ∀ x ∈ [ -π/4 ; π/3 ]
a.
Đặt \(cos2x=t\Rightarrow t\in\left[-1;1\right]\)
Xét hàm \(y=f\left(t\right)=2t^2+2t-4\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\in\left[-1;1\right]\)
\(f\left(-1\right)=-4\) ; \(f\left(-\dfrac{1}{2}\right)=-\dfrac{9}{2}\) ; \(f\left(1\right)=0\)
\(\Rightarrow y_{min}=-\dfrac{9}{2}\) khi \(t=-\dfrac{1}{2}\) hay \(cos2x=-\dfrac{1}{2}\)
\(y_{max}=0\) khi \(cos2x=1\)
b. Đặt \(tanx=t\Rightarrow t\in\left[-1;\sqrt{3}\right]\)
Xét hàm \(f\left(t\right)=t^2-2\sqrt{3}t-1\) trên \(\left[-1;\sqrt{3}\right]\)
\(-\dfrac{b}{2a}=\sqrt{3}\in\left[-1;\sqrt{3}\right]\)
\(f\left(-1\right)=2\sqrt{3}\) ; \(f\left(\sqrt{3}\right)=-4\)
\(y_{min}=-4\) khi \(x=\dfrac{\pi}{3}\) ; \(y_{max}=2\sqrt{3}\) khi \(x=-\dfrac{\pi}{4}\)
Tìm góc α ∈ {π/6;π/4;π/3;π/2} để phương trình cos2x+ 3 sin2x-2cosx= 0 tương đương với phương trình c o s ( 2 x - α ) = cos x
A. α = π / 6
B. α = π / 4
C. α = π / 2
D. α = π / 3
Khi đặt hiệu điện thế không đổi 30 V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm 1/4 π (H) thì dòng điện trong đoạn mạch là dòng điộn một chiều có cường độ 1 A. Nếu đặt vào hai đầu đoạn mạch này điện áp xoay chiều u = 150.1/ π .cos120 π t(V) thì biểu thức của cường độ dòng điện trong đoạn mạch là :
A. i = 5 2 cos(120 π t + π /4) (A).
B. i = 5 2 cos(120 π t - π /4) (A).
C. i = 5cos(120 π t - π /4) (A).
D. i = 5cos(120 π t + π /4) (A).
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó:
V H V ABCD . A ' B ' C ' D '
A. π /6 B. π /4
C. π /3 D. π /( 3 )
Chọn A.
Gọi 2a là cạnh của hình lập phương thì hình cầu nội tiếp hình lập phương đó có bán kính r = a.
Suy ra:
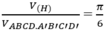
Tổng các nghiệm của phương trình: sin 2 ( 2 x - π / 4 ) - 3 cos ( 3 π / 4 - 2 x ) + 2 = 0 ( 1 ) trong khoảng (0;2π) là:
A. 7π/8
B. 3π/8
C. π
D. 7π/4
Tính cos(α-π/3) biết sinα=3/5 và π/2
Lời giải:
$\cos^2 a=1-\sin^2a=1-(\frac{3}{5})^2=\frac{16}{25}$
$\Rightarrow \cos a=\pm \frac{4}{5}$
Ta có:
\(\cos (a-\frac{\pi}{3})=\cos a\cos \frac{\pi}{3}-\sin a\sin \frac{\pi}{3}\)
\(=\frac{1}{2}\cos a-\frac{3\sqrt{3}}{10}=\frac{1}{2}.\pm \frac{4}{5}-\frac{3\sqrt{3}}{10}\)