cho đường thẳng A và song song với BC cắt đường thẳng qua C và song song với AB tại D. Chứng minh rằng: AB=CD, BC=AD
giúp mik với mik đang cần gấp![]()
Cho ∆ABC,D là trung điểm của cạnh AB,đường thẳng kẻ qua D và song song với cạnh BC cắt AC ở E,đường thẳng kẻ qua E và song song với AB cắt BC tại F . Chứng minh rằng a.AE = EC;BF=FC b.DE=1/2 BC;EF = 1/2 AB
Mình đang cần gấp ạ!
a: Xét ΔABC có
D là trung điểm của AB
DE//BC
=>E là trung điểm của AC
=>AE=EC
Xét ΔCAB có
E là trung điểm của CA
EF//AB
=>F là trung điểm của BC
=>FB=FC
b: Xét ΔABC có D,E lần lượt là trung điểm của AB,AC
nên DE là đường trung bình
=>ED=1/2BC
Xét ΔCAB có CF/CB=CE/CA
nên EF//AB
=>FE/AB=CF/CB=1/2
=>FE=1/2AB
Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng :
a) AD = EF
b) Tam giác ADE = Tam giác EFC
c) AE = EC
mk đang cần gấp
c: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
: Cho hình thang ABCD (AB < CD và AB // CD). Vẽ qua A đường thẳng AK song song với BC (K DC) và AK cắt BD tại E, vẽ qua B đường thẳng BI song song với AD (I CD) cắt AC tại F.
a) Chứng minh rằng: EF // AB
b) Chứng minh rằng: AB2 = CD.EF
Cho tam giác ABC, trên cạnh AB và AC lấy các điểm tương ứng D và E. Đường thẳng song song với AC qua D cắt BE tại I, đường thẳng song song với AB qua E cắt CD tại K. Chứng minh rằng IK // BC.
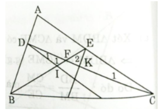
Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
![]()
Tương tự ta có: ΔDFB ∼ ΔKFE
![]()
Từ (1), (2) ⇒ FC.FI = FB.FK
![]()
Do đó theo định lí Talét đảo ta có KI // BC.
Cho hình thang ABCD, đáy AB. Từ đỉnh C, kẻ đường thẳng song song với AD, đường này cắt BD tại P và cắt AB tại E. Qua D, kẻ đường thẳng song song với BC, đường này cắt AC tại N và AB tại F. Đường thẳng qua E, song song với AC cắt BC tại Q và đường thẳng qua F song song với BD cắt AD tại M
a, Chứng minh bốn điểm M,N,P,Q nằm trên 1 đường thẳng song song với hai đáy
b, Chứng minh: MN = PQ
c, Cho AB=a, CD=b. Chứng minh rằng các điểm M, N,P, Q theo thứ tự chia các đoạn thẳng AD, AC, BD, DC theo cùng 1 tỉ số k. Tính k theo a và b.
Cho tam giác ABC . Đường thẳng qua A và song song với BC cắt đường thẳng qua C và song song với AB tại D .
a) Chứng minh rằng: tam giác ABC = tam giác CDA . Từ đó suy ra AB = CD , BC = AD
b) Gọi M và N lần lượt là trung điểm của AD và BC . Cho MN và AC cắt nhau tại I . Chứng minh rằng: IM = IN .
a: Xét tứ giác ABCD có
AD//BC
AB//CD
Do đó: ABCD là hình bình hành
Suy ra: AB=CD
Cho tam giác ABC. Đường thẳng qua A song song với BC cắt đường thẳng qua C và song song với AB tại D. Chứng minh AB = CD và BC = AD
???? Đề nó có bị nhầm lẫn j ko bn???
Vì \(AD\) // \(BC\left(gt\right)\)
=> \(\widehat{DAC}=\widehat{ACB}\) (vì 2 góc so le trong)
Vì \(AB\) // \(CD\left(gt\right)\)
=> \(\widehat{BAC}=\widehat{ACD}\) (vì 2 góc so le trong)
Xét 2 \(\Delta\) \(ABC\) và \(CDA\) có:
\(\widehat{ACB}=\widehat{DAC}\left(cmt\right)\)
\(\widehat{BAC}=\widehat{ACD}\left(cmt\right)\)
Cạnh AC chung
=> \(\Delta ABC=\Delta CDA\left(g-c-g\right).\)
=> \(\left\{{}\begin{matrix}AB=CD\\BC=AD\end{matrix}\right.\) (2 cạnh tương ứng).
Chúc bạn học tốt!
Xét tam giác ABC và tam giác CDA có :
^BAC=^ACD ( 2 góc so le trong )
AC chung
^BCA=^CAD ( 2 góc so le trong )
=> tam giác ABC = tam giác CDA ( g.c.g )
AB = CD ( 2 cạnh tương ứng )
BC = AD ( 2 cạnh tương ứng )
Cho hình thang ABCD, O là giao điểm của 2 đường chéo, đáy lớn CD. Đường thẳng qua A song song với BC cắt BD ở E và đường thẳng qua B song song với AD cắt đường thẳng AC tại F.
a) CHứng minh: EF song song với AB.
b) Chứng minh: AB^2=EF.CD
c) Gọi S1, S2, S3, S4 theo thứ tự là diện tích các tam giác CAB, OCD, OAD, OBC. Chứng minh: S1.S2=S3.S4
Cho ∆ABC ,D là trung điểm AB , đường thẳng qua D và song song với BC cắt AC tại E , qua E kẻ đường thẳng song song với AB và BC cắt BC tại F . Chứng minh rằng :
a) BD = EF
b) E là trung điểm của AC
c) DF || AC
d) DF = 1/2 AC
Mọi người vẽ hình và ghi giả thiết và kết luận hộ mình nha xin mọi người giải hộ mình đó mình đang cần gấp
Cứng đờ tay luôn rồi, khổ quá:((
a) Xét ΔDBFΔDBF và ΔFED:ΔFED:
DF:cạnh chung
ˆBDF=ˆEFDBDF^=EFD^(AB//EF)
ˆBFD=ˆEDFBFD^=EDF^(DE//BC)
=> ΔBDF=ΔEFD(g−c−g)ΔBDF=ΔEFD(g−c−g)
b) (Ở lớp 8 thì sé có cái đường trung bình ý bạn, nó sẽ có tính chất luôn, nhưng lớp 7 chưa học đành làm theo lớp 7 vậy)
Ta có: ˆDAE+ˆAED+ˆEDA=180oDAE^+AED^+EDA^=180o (Tổng 3 góc trong 1 tam giác)
Lại có: ˆAED+ˆDEF+ˆFEC=180oAED^+DEF^+FEC^=180o
Mà ˆDEF=ˆEDADEF^=EDA^(AB//EF)
=>ˆDAE=ˆFECDAE^=FEC^
Xét ΔDAEΔDAE và ΔFEC:ΔFEC:
DA=FE(=BD)
ˆDAE=ˆEFC(=ˆDBF)DAE^=EFC^(=DBF^)
ˆDAE=ˆFECDAE^=FEC^ (cmt)
=>ΔDAE=ΔFEC(g−c−g)ΔDAE=ΔFEC(g−c−g)
=> DE=FC(2 cạnh t/ứ)
=> Đpcm