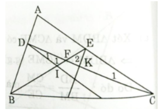
Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
![]()
Tương tự ta có: ΔDFB ∼ ΔKFE
![]()
Từ (1), (2) ⇒ FC.FI = FB.FK
![]()
Do đó theo định lí Talét đảo ta có KI // BC.

Gọi F là giao điểm của BE và CD.
Ta có DI // AC (gt) ⇒ ∠D1 = ∠C1 (so le trong)
và ∠F1 = ∠F2 (đối đỉnh)
Do đó: ΔDFI ∼ ΔCFE (g.g)
![]()
Tương tự ta có: ΔDFB ∼ ΔKFE
![]()
Từ (1), (2) ⇒ FC.FI = FB.FK
![]()
Do đó theo định lí Talét đảo ta có KI // BC.
Tam giác ABC, trên AB, AC lấy D,E. Qua D, kẻ đường thẳng song song với AC cắt BE tại I. Qua E, iker đường thẳng song song với AB cắt CD tại K.
Chứng minh: IK // BC
Cho tam giác ABC trên cạnh AB và AC lần lượt lấy các điểm D và E. Đường thẳng song song với AC qua D cắt BE tại I. Đường thẳng song song với AB qua E cắt CD tại K. Gọi F là giao điểm của BE và CD. Chứng minh:
a) Tam giác DFI đồng dạng với tam giác CFE
b) Tam giác DFB đồng dạng với tam giác KFE
c) KI//BC
toán lớp 8cho tam giác abc .trên cạnh ab và ac lần lượt lấy các điểm d và e. bd ,ce cắt nhau tại f. qua tam giác vẽ đường thẳng song song với ac cắt be tại i, qua e kẻ đường thẳng song song ab cắt cd tại k.chứng minh: a) fi/fd=fe/fc b)fbxfk=fdxfe c)ik//bc
cho tam giác cân ABC (CA=CB) đường cao BD. trên các cạnh BA, BC lấy tương ứng hai điểm E và F sao cho BE=BF=BD. qua E kẻ đường thẳng song song với AC cắt BC ở N, cắt BD tại K. qua F kẻ đường thẳng song song với AC cắt AB tại M, cắt BD tại I
Tính độ dài các canh AB, BC nếu biết EM= 9cm, FN=12cm, IK= 6cm
1) Cho tam giác ABC có phân giác AD và trung tuyến BE cắt nhau tại O. Đường thẳng qua O và song song với AC cắt AB và BA lần lượt tại M và N. Tình độ dài các cạnh AB và BC, biết rằng AM=12cm, AC=40cm, CN=14cm
2)cho tam giác ABC cân tại A có CD đường cao. Trên các cạnh CB và CA lấy các điểm E và F sao cho DC=CE=CF. Đường thẳng qua E song song với AB cắt CD tại K và AC tại N, đường thẳng qua F và song song với AB cắt BC tại M. Tính độ dài các cạnh tam giác ABC, biết rằng EM=9cm, FN=12cm, IK=6cm
3)Cho hình thang cân ABCD(AB//CD). Đường cao AH cắt đường chéo BD tại K. AD và BC cắt nhau tại M. Tính độ dài AM, biết rằng AD=20cm, DK/KB=2/3.
Bài 6: Cho hình thang ABCD có hai đáy là AB và CD. Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E và F.
a) Chứng minh ED/AD + BF/BC = 1
b) Các đường chéo của hình thang cắt nhau tại O. Chứng minh OA.OD = OB.OC.
Bài 7: Cho tam giác ABC nhọn, M là trung điểm của BC, E thuộc đoạn thẳng MC. Qua E kẻ đường thẳng song song với AC cắt AB ở D, cắt AM ở K. Qua E kẻ đường thẳng song song với AB cắt AC ở F.
a) Chứng minh CF = DK
b) Gọi H là trực tâm của tam giác ABC. Đường thẳng qua H vuông góc với MH cắt AB và AC theo thứ tự ở I và K’. Qua C kẻ đường thẳng song song với IK’, cắt AH và AB theo thứ tự ở N và P. Chứng minh NC = NP và HI = HK’.
Bài 8: Cho tam giác ABC, điểm M bất kì trên cạnh AB. Qua M kẻ đường thẳng song song với BC cắt AC ở N biết AM = 11 cm, MB = 8 cm, AC = 38 cm. Tính độ dài các đoạn thẳng AN, NC.
Bài 9: Cho góc xAy, trên tia Ax lấy hai điểm D và E, trên tia Ay lấy hai điểm F và G sao cho FD song song với EG. Đường thẳng qua G song song với FE cắt tia Ax tại H. Chứng minh AE 2 = AD.AH.
Bài 10: Cho hình bình hành ABCD. Gọi E là một điểm bất kì trên cạnh AB. Qua E kẻ đường thẳng song song với AC cắt BC ở F và kẻ đường thẳng song song với BD cắt AD ở H. Đường thẳng kẻ quá F song song với BD cắt CD ở G. Chứng minh AH.CD = AD.CG.
Cho tam giác cân ABC (CA = CB), đường cao BD. Trên các cạnh BA, BC lấy tương ứng hai điểm E và F sao cho BE = BF = BD. Qua E kẻ đường thẳng song song với AC cắt BC ở N, cắt BD ở K. Qua F kẻ đường thẳng song song với AC cắt AB ở M, cắt BD ở I.
Tính độ dài các cạnh AB, BC nếu biết EM = 9cm, FN = 12cm và IK = 6cm.
Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB, AC tại D và E. Qua C kẻ đường thẳng song song với AB cắt DE tại F. Gọi H là giao điểm của AC với BF. Đường thẳng qua H song song với AB cắt BC tại I. Chứng minh rằng:
a. DA/DB = ED/FE
b. HA.HE = HC2
cho tam giác ABC, kẻ một đường thẳng song song với cạnh BC cắt hai cạnh AB và AC thứ tự tại D và E, gọi O là giao điểm của BE và CD, qua O kẻ đường thẳng song song với BC cắt BD tại M. Chứng minh rằng:
1) OB.OD=OC.OE
2)