Cho hàm số f x = 1 3 x 3 − m x + 2 , m là tham số. Biết hàm số có hai điểm cực trị x 1 , x 2 . Tìm giá trị nhỏ nhất của biểu thức T = x 1 2 + x 2 2 − 10 x 1 + x 2
A. -1
B. 1
C. -18
D. -22
1/ Cho hàm số \(f\)(\(x\))=\(\dfrac{1}{3}\)\(x\)\(^3\)+\(x \)\(^2\)-(\(m\)+1)\(x\)-\(m\)+3. Với \(m\) là tham số. Có bao nhiêu số nguyên \(m\) thuộc đoạn [-10;10] để \(f\)'(\(x\)) ≥ 0, ∀\(x\) ϵ \(R\)
2/ Cho hàm số \(y\) = \(\dfrac{mx+4}{x+m}\). Với \(m\) là tham số. Có bao nhiêu số nguyên m thuộc đoạn [-5;2023] để \(y\)' > 0, ∀\(x\) ϵ (0;+∞).
1: \(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2+2x-\left(m+1\right)=x^2+2x-m-1\)
\(\Delta=2^2-4\left(-m-1\right)=4m+8\)
Để f'(x)>=0 với mọi x thì 4m+8<=0 và 1>0
=>m<=-2
=>\(m\in\left\{-10;-9;...;-2\right\}\)
=>Có 9 số
Cho hàm số y = f(x) xác định trên tập số thực R và có đạo hàm f'(x) = (x - sinx)(x- m- 3)(x- \(\sqrt{9-m^2}\) )3 ∀x∈ R (m là tham số). Có bao nhiêu giá trị nguyên của m để hàm số y =f(x) đạt cực tiểu tại x = 0
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
Cho hàm số y=f(x)=√x+7 -3∠x-2 , xkhác 2 ; mx+2023 ,x=2 (với m là tham số)
Tìm m để hàm số liên tục tại điểm x=2
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{x+7}-3}{x-2}\left(x< >2\right)\\mx+2023\left(x=2\right)\end{matrix}\right.\)
Để hàm số liên tục tại x=2 thì \(\lim\limits_{x\rightarrow2}f\left(x\right)=F\left(2\right)\)
=>\(\lim\limits_{x\rightarrow2}\dfrac{x+7-9}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=2m+2023\)
=>\(2m+2023=\dfrac{1}{\sqrt{2+7}+3}=\dfrac{1}{6}\)
=>m=-12137/12
tìm điều kiện của tham số m để f(x)=x^3+(m^2-1)x^2+3x+m+1 là hàm số lẻ
Cho hàm số
f
(
x
)
=
x
3
3
+
(
4
-
m
)
x
2
2
+
(
5
-
2
m
)
x
+
m
2
+
3
,
với m là tham số thực.
Hàm số
g
(
x
)
=
x
2
+
4
x
+
5
x
+
2
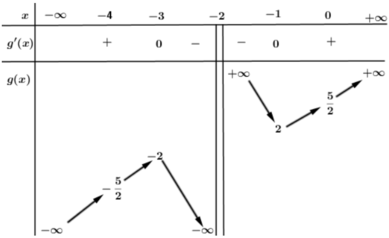
có đồ thị C và bảng biến thiên sau:
Tìm m sao cho hàm số f(x) đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1
A. m> 2
B. 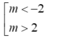
C. m < -5/2
D. m> 5 2
Xét phương trình f’ (x) = x2+(4-m) x+5-2m=0
⇔ x 2 + 4 x + 5 = m ( x + 2 ) ⇔ g ( x ) = x 2 + 4 x + 5 x + 2 = m
Ta có nghiệm của f’ (x)=0 cũng là hoành độ giao điểm của g(x)=m
Khi đó từ bảng biến thiên ta có YCBT khi m> 2.
Chọn A.
Cho hàm số f(x)=3 sinx+2. Gọi S là tập hợp các giá trị nguyên của tham số m để hàm số y = f 3 ( x ) - 3 mf 2 ( x ) + 3 ( m 2 - 4 ) f ( x ) - m nghịch biến trên khoảng (0;π/2). Số tập con của S bằng
A. 1
B. 2.
C. 4.
D. 16.
Cho hàm số f(x) = (m - 1)x3 - 5x2 + (m+3)x + 3. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f(\(\left|x\right|\)) có đúng 3 điểm cực trị?
- Với \(m=1\) thỏa mãn
- Với \(m\ne1\):
\(f'\left(x\right)=3\left(m-1\right)x^2-10x+m+3\)
\(f\left(\left|x\right|\right)\) có số cực trị bằng \(2k+1\) với \(k\) là số cực trị dương của \(f\left(x\right)\) nên hàm có 3 cực trị khi \(f'\left(x\right)=0\) có đúng 1 nghiệm dương
TH1: \(f'\left(x\right)=0\) có 1 nghiệm bằng 0 \(\Rightarrow m=-3\Rightarrow f'\left(x\right)=-12x^2-10x\) ko có nghiệm dương (loại)
TH2: \(f'\left(x\right)=0\) ko có nghiệm bằng 0 nào \(\Rightarrow f'\left(x\right)=0\) khi và chỉ khi nó có 2 nghiệm trái dấu
\(\Rightarrow ac< 0\Leftrightarrow3\left(m-1\right)\left(m+3\right)< 0\)
\(\Rightarrow-3< m< 1\)
Vậy \(-3< m\le1\)
Cho hàm số f(x)=(2 x +m)/(√x+1) với m là tham số thực, m>1. Gọi S là tập tất cả các giá trị nguyên dương của m để hàm số có giá trị lớn nhất trên đoạn [0;4] nhỏ hơn 3. Số phần tử của tập S là
A. 1
B. 3
C. 0
D. 2
Cho hàm số y=f(x)=\(3\sqrt{x+1}+mx^2-2x+3\)với m là tham số.
Tìm m để \(f\left(3\right)=f\left(-1\right)\)
Cho hàm số y=f(x)=\(\left\{{}\begin{matrix}2x^3-3\left(m+1\right)x^2+6mx-2\left(x< =3\right)\\nx+46\left(x>3\right)\end{matrix}\right.\)
trong đó m,n thuộc R. Tính tổng tất cả các giá trị nguyên của tham số m để hàm số y=f(x) có đúng ba điểm cực trị
- Với \(x< 3\Rightarrow f'\left(x\right)=6x^2-6\left(m+1\right)x+6m=6\left(x-1\right)\left(x-m\right)\)
\(f'\left(x\right)=0\Rightarrow6\left(x-1\right)\left(x-m\right)=0\left(1\right)\Rightarrow\left[{}\begin{matrix}x=1\\x=m\end{matrix}\right.\) có tối đa 2 cực trị khi \(x< 3\)
- Với \(x>3\Rightarrow f'\left(x\right)=n\) là hằng số \(\Rightarrow f\left(x\right)\) ko có cực trị khi \(x>3\)
\(\Rightarrow\) Hàm có đúng 3 điểm cực trị khi và chỉ khi nó đồng thời thỏa mãn:
ĐK1: \(f'\left(x\right)=0\) có 2 nghiệm pb khi \(x< 3\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ne1\end{matrix}\right.\)
ĐK2: \(x=3\) là 1 cực trị của hàm số
\(\Rightarrow f\left(x\right)\) liên tục tại \(x=3\) đồng thời đạo hàm đổi dấu khi đi qua \(x=3\)
\(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)\Leftrightarrow3n+46=25-9m\Rightarrow n=-3m-7\) (2)
Mặt khác do 2 nghiệm của (1) đều nhỏ hơn 3 \(\Rightarrow\) tại lân cận trái của \(x=3\) đạo hàm luôn có dấu dương
\(\Rightarrow\) Để đạo hàm đổi dấu khi đi qua \(x=3\) thì \(f'\left(3^+\right)=n< 0\)
Thế vào (2) \(\Rightarrow-3m-7< 0\Rightarrow m>-\dfrac{7}{3}\)
\(\Rightarrow-\dfrac{7}{3}< m< 3\Rightarrow\sum m=0\)