Cho (C): y = m x 4 - ( m 2 - 3 ) x 2 + m - 2 . Tìm m để (C) có 2 điểm cực tiểu và 1 điểm cực đại đồng thời y C Đ < 0
![]()
![]()
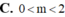
![]()
(1 điểm) Cho các số thực dương ${x}, \, {y}$ thỏa mãn: $\sqrt{y}(y+1)-6 x-9=(2 x+4) \sqrt{2 x+3}-3 y$.
Tìm giá trị lớn nhất của biểu thức $M=x y+3 y-4 x^{2}-3$.
Bài hơi nhiều n cũng mong mn làm hết cho m . thanks
Bài 9:
a, (x+3)(x+4)
b,(x-4)(x2+4x+16)
c,(xy2-1)(x2y+5)
d,4(x-1/2)(x+1/2)(4x2+1)
Bài 10:
Cho biểu thức:
P=(m2-2m+4)(m+2)-m3+(m+3)(m-3)-m2 -18
CM biểu thức P=(x+y)3 -9(x+y)2 +27(x+y)-27
ko thuộc vào m
Bài 11:
a, (x2+2x+4)(2-x)+x(x-3)(x+4)-x2+24=0
b, (x/2+3)(5-6x)+(12x-2)(x/4+3)=0
Bài 12:
CM rằng với mọi x,y ta luôn có:
(x4-x3y+x2y2-xy3+y4)(x+y)=x5+y5
Bài 13:
Tìm 2 số lẻ liên tiếp , biết bình phương của số lớn, lớn hơn bình phương của số nhỏ là 80 đơn vị
Bài 14*:
Cho a và b là 2 số tự nhiên thỏa mãn (a+3) và (b+4) cùng chia hết cho 5. CM a2+b2 cũng chia hết cho 5.
c)\(\left(xy^2-1\right)\left(x^2y+5\right)\)
\(=x^3y^3+5xy^2-x^2y-5\)
d)\(4\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)\left(4x^2+1\right)\)
\(=4\left(x^2-\dfrac{1}{4}\right)\left(4x^2+1\right)\)
\(=4\left(4x^4+x^2-x-\dfrac{1}{4}\right)\)
\(=16x^4+4x^2-4x-1\)
Bài 9
a)\(\left(x+3\right)\left(x+4\right)\) b)\(\left(x-4\right)\left(x^2+4x+16\right)\)
\(=x^2+4x+3x+12\) \(=\left(x-4\right)\left(x^2+x.4+4^2\right)\)
\(=x^2+7x+12\) \(=x^3-4^3=x^3-64\)
bài 13
Tìm 2 số lẻ liên tiếp,biết bình phương số lơn lớn hơn bình phương số nhỏ là 80 đơn vị
2 số lẻ liên tiếp,biết bình phương số lơn lớn hơn bình phương số nhỏ là 80 đơn vị là :
19^2 và 21^2
Mọi người giúp mình với mình đang vội!Cảm ơn
1,rút gọn các biểu thức sau
a, x.(x+2)^2 +(x-3).(x^2+3x+9)
b,(a+b).(a^2 -a.b+b^2)-2a.(a-b)^2
c,(x-1)^3 -(x+2).9x^2-2x+4)+3.(x+4).(x-4)
d,(2x-5)^3-(x-3)^3+(2x-5).(4x^2+10x+25)
e,(x^2-xy+y^2).(x-y).(x^2+xy+y^2).(x+y)
2.Cho 2 đơn thức A=(2ax^2y^3)^2 và \B= -1/3 bx^#y )a,b hằng số khác 0)
Tính M=A.B Tìm B của M
b,Cho 2 đa thức C(x) sao cho C(x)+B(x)= -A(x)
1. Tìm các số nguyên tố x,y sao cho: 51x + 26y = 2000
2. Tìm số tự nhiên x, y biết: 7(x - 2004)^2 = 23 - y^2
3. Tìm x,y nguyên biết: 2xy - x -y=2
4. tìm x, biết |x+1,1| +|x+1,2|+|x+1,3|+|x+1,4|=5x
5, Tìm các số x,y,z biết: x/2=y/3=z/4 và x^2 + y^2 + z^2 = 116
6. Tìm các số x,y,z biết: 2x-3y/2=4y-2z/3=3z-4x/4 và 3x+2y+z=17
1, https://hoc24.vn//hoi-dap/question/91350.html
Bài 3:
=>2xy-x-y-2=0
=>x(2y-1)-y+0,5-2,5=0
=>x(2y-1)-(y-0,5)=2,5
=>2x(2y-1)-(2y-1)=5
=>(2y-1)(2x-1)=5
=>\(\left(2x-1;2y-1\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(0;-2\right);\left(-2;0\right)\right\}\)
Câu 5:
Đặt x/2=y/3=z/4=k
=>x=2k; y=3k; z=4k
x^2+y^2+z^2=116
=>4k^2+9k^2+16k^2=116
=>29k^2=116
=>k^2=4
TH1: k=2
=>x=4; y=6; z=8
TH2: k=-2
=>x=-4; y=-6; z=-8
a) Cho a,b,c độ dài 3 cạnh của một tam giác
C/m a^3+ab^3-abc^2+2a^2b^2 >0
b) cho x+y+z=0.
C/m x^4+y^4+z^4=2(x^2y^2+y^2z^2+z^2x^2)
, Cho hàm số y=x-1/x^2+mx+4. Tìm m để đồ thị hàm số có 2 đường tiện cận 13, tìm m để(C):y= mx^3-x^2-2x+8m cắt Ox tại 3 điểm phân biệt có Hoành độ âm 14,cho (C) :y= x^3+(m+2) x+1 d:y= 2x-1 Tìm m để d cắt C tại 1 điểm duy nhất có Hoành độ dương 15, tìm m để phương trình -x^4+2x^2+3x+2m=0 có 3 nghiệm phân biệt
Câu 1:
Cho M = 1+3+3^2+3^3+3^4+...+3^99+3^100. Tìm số dư khi chia M cho13, Chia M cho 14
Câu 2:
Cho A= 4^0+4^1+4^2+...+4^2016
Câu 3:Tìm x và y biết
/x/+/y/=25
Câu 1: Câu hỏi của masrur chỉ có số dư khi chia M cho 13 nhưng bạn áp dụng thêm để ra M chia cho 14
Câu 2: Đề thiếu
Câu 3: Đề không tồn tại
1....cho hàm số y=-x3+3x2 -4 (C). Tìm m để đường thẳng d: y=m(x+1) cắt đồ thị (C) tại 3 điểm M(-1;0), B, C sao cho MA=2MB
2....Cho hàm số y=\(\frac{2x}{x+1}\) (C). Tìm 2 điểm thuộc (C) đối xứng qua d: 2x +y - 4 =0
3.... Cho h số y+\(\frac{x^2-2x+2}{x-1}\) (C).Tìm m để đường thẳng d: y= -x +m cắt (C) tại 2 điểm đối xứng nhau qua đường thẳng y = x+3
1/Cho x,y là các số thực dương thỏa mãn: x+y≤4. Tìm GTNN \(P=\dfrac{x^4}{\left(y-1\right)^3}+\dfrac{y^4}{\left(x-1\right)^3}\)
2/ Cho x,y,z nguyên thỏa mãn :x+y+z=2013.Chứng minh:
\(Q=\left(x^2+xy+yz\right)^3+\left(y^2+yz+xz\right)^3+\left(z^2+xz+xy\right)^3⋮3\)