Trong các đường thẳng sau, đường thẳng nào tiếp xúc với đồ thị ( C ) : y = 2 x 4 - 4 x 2 + 1 tại hai điểm phân biệt?
![]()
![]()
![]()
Trong các đường thẳng sau, đường thẳng nào là đường thẳng đi qua điểm A(3;0) và tiếp xúc với đồ thị hàm số y=-1/3 x^3 +3x ?
A. y = 2 5 x + 7 5
B. y = - 3 4 x + 9 4
C. y = 6 x - 18
D. y = - 6 x + 18
Gọi (P) là đồ thị hàm số y = 2 x 3 - x + 3 . Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của (P)?
A. y = -x-3
B. y = 11x+4
C. y = -x+3
D. y = 4x-1
Chọn C.
![]()
Điều kiện để đường thẳng y = ax + b là tiếp tuyến của hàm số y = f(x) (C):
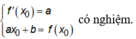
Kiểm tra các đáp án
Đáp án A
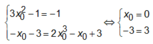
vô lí, đáp án A sai.
Đáp án B:
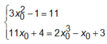
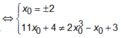
đáp án B sai.
Đáp án C:
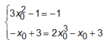
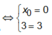
luôn đúng. Đáp án C đúng.
Do đáp án C đúng nên đáp án D sai.
Gọi (P) là đồ thị hàm số y = 2 x 3 - x + 3 . Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của (P)?
A. y = - x - 3
B. y = 11 x + 4
C. y = - x + 3
D. y = 4 x - 1
1 vẽ đồ thị hàm số y= x²/2 (P) 2 bằng phép tính hãy xác định toạ độ các giáo điểm parabol (P) với đưownhf thẳng (d) có phương trình y=-1/2 x+1 3 với các giá trị nào của m thì đường thẳng (d) y=X+m a cắt parabol (P) b tiếp xúc với parabol c không cắt parabol
Cho parabol: \(y=\dfrac{-x^2}{4}\) và đường thẳng y=mx+n. Xác định các hệ số m và n để đường thẳng đi qua điểm (1;2) và tiếp xúc với parabol. Tìm tọa độ tiếp điểm, vẽ đồ thị của parabol và đường thẳng trên cùng 1 hệ trục tọa độ
Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{4}x^2-mx-n=0\)
THeo đề, ta có:
\(\left\{{}\begin{matrix}m+n=2\\\left(-m\right)^2-4\cdot\left(-\dfrac{1}{4}\right)\cdot\left(-n\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\m^2-n=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\n^2-4n+4-n=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n\in\left\{1;4\right\}\\m\in\left\{1;-2\right\}\end{matrix}\right.\)
Đồ thị \(y=\frac{x^2}{2}\)
Với giá trị nào của m thì đường thẳng y=x-m tiếp xúc (P)
Cho hàm số 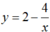 có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
A. y = x + 4.
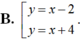
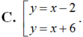
D. Không tồn tại.
Chọn C.
Đạo hàm: 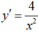
Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.
Ta có phương trình 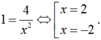
Tại M(2; 0). Phương trình tiếp tuyến là y = x – 2.
Tại N(-2; 4). Phương trình tiếp tuyến là y = x + 6.
Tìm m để đường thẳng (d): \(y=mx+4\) tiếp xúc với đồ thị hàm số (P): \(\dfrac{-x^2}{4}\) .
(hai đồ thị hàm số tiếp xúc nhau là hai đồ thị chỉ có 1 điểm chung)
Giúp mk làm bài này với
Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{4}x^2-mx-4=0\)
\(\Leftrightarrow x^2+4mx+16=0\)
\(\Delta=\left(4m\right)^2-4\cdot1\cdot16=16m^2-64\)
Để hai đồ thị tiếp xúc với nhau thì 16m2-64=0
=>m=2 hoặc m=-2
Trong các đường thẳng sau, đường thẳng nào là tiếp tuyến của đồ thị hàm số y = 2 x + 3 x + 2 chắn hai trục tọa độ một tam giác vuông cân
A. y = x + 2
B. y = x - 2
C. y = - x + 2
D. y = 1 4 x + 3 2