Biết đường thẳng (d): y=x-1 là tiếp tuyến của (C): y = x - 1 2 x - 1 . Tìm tung độ y M của tiếp điểm.
![]()
![]()
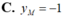
![]()
Cho hàm số 3 2 y x x = − +3 có đồ thị (C) . Gọi 1 d , 2 d là tiếp tuyến của đồ thị (C) vuông góc với đường thẳng x y − + = 9 1 0 . Tính khoảng cách giữa hai đường thẳng 1 d , 2 d .
Cho hàm số \(y=f\left(x\right)=\dfrac{x-2}{x+1}\) có đồ thị (C). Viết phương trình tiếp tuyến của đồ thị (C) biết tiếp tuyến cắt 2 đường thẳng d1:x=-1 và d2:y=1 lần lượt tại A, B sao cho bán kính đường tròn nội tiếp tam giác IAB là lớn nhất.
Cho hàm số \(y=-x^4-x^2-1\left(C\right)\). Viết phương trình tiếp tuyến của (C), biết :
a) Tiếp tuyến vuông góc với đường thẳng \(d:y=x-6y-1=0\)
b) Tiếp tuyến song song với đường thẳng \(d':y=6x+2\)
Ta có \(y'=-4x^3-2x\)
a) Vì tiếp tuyến vuông góc với đường thẳng \(d:y=\frac{1}{6}x-\frac{1}{6}\)
Suy ra \(y'\left(x_0\right)=-6\Leftrightarrow2x_0^3+x_0^2-3=0\Leftrightarrow x_0=1\Rightarrow y_0=-3\)
Phương trình tiếp tuyến là \(y=-6x+3\)
b) Vì tuyến tuyến song song với đường thẳng \(y=6x+2\) nên ta có :
\(y'\left(x_0\right)=6\Leftrightarrow2x_0^3+x_0^2+3=0\Leftrightarrow\left(x_0+1\right)\left(2x_0^2-2x_0+3\right)=0\Rightarrow x_0=-1\Rightarrow y_0=-3\)
Nên ta có phương trình tiếp tuyến là :
\(y=6\left(x+1\right)-3=6x+3\)
Cho hàm số \(y=x^3+3x^2-6x+1\) (C)
Viết pt tiếp tuyến của đồ thị (C) biết tiếp tuyến vuông góc với đường thẳng \(y=-\dfrac{1}{18}x+1\) ?
\(y'=3x^2+6x-6\)
Tiếp tuyến vuông góc đường thẳng đã cho nên có hệ số góc thỏa mãn:
\(k.\left(-\dfrac{1}{18}\right)=-1\Rightarrow k=18\)
\(\Rightarrow3x^2+6x-6=18\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow y=9\\x=-4\Rightarrow y=9\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=18\left(x-2\right)+9\\y=18\left(x+4\right)+9\end{matrix}\right.\)
Cho đường tròn (C): (x-1)2 + (y+2)2=5 và M (3;-1)
a. Viết phương trình tiếp tuyến của (C) tại M
b.Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng: x+2y-1=0
a, Phương trình tiếp tuyến đi qua M: \(ax+by-3a+b=0\left(\Delta\right)\)
Đường tròn đã cho có tâm \(I=\left(1;-2\right)\) bán kính \(R=\sqrt{5}\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|a-2b-3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{5}\)
\(\Leftrightarrow\left(2a+b\right)^2=5\left(a^2+b^2\right)\)
\(\Leftrightarrow\left(a-2b\right)^2=0\)
\(\Leftrightarrow a=2b\)
\(\Rightarrow\Delta:2x+y-5=0\)
b, Phương trình tiếp tuyến: \(\left(d\right)2x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;d\right)=\dfrac{\left|2.1-1.\left(-2\right)+m\right|}{\sqrt{5}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+4\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-9\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}d:2x-y+1=0\\d:2x-y-9=0\end{matrix}\right.\)
Cho đường tròn (C) : (x- 3) 2+ (y +1) 2= 5. Phương trình tiếp tuyến của (C) song song với đường thẳng d : 2x+ y + 5 = 0 là:
A . 2x+ y= 0 và 2x+ y -10= 0
B. 2x+ y= 2= 0 và 2x+ y-8= 0
C. 2x+ y+ 10 =0 và 2x+ y= 0
D. 2x+ y-10= 0
Đáp án A
Phương trình tiếp tuyến có dạng
∆: 2x+ y+ m= 0.
Đường tròn (C) :
(x- 3) 2+ (y +1) 2= 5 có tâm I( 3; -1) và bán kính ![]()
Đường thẳng tiếp xúc với đường tròn (C) khi
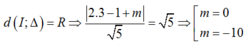
Vậy có 2 đường thẳng thỏa mãn là:
2x+ y= 0 và 2x+ y -10= 0
Cho đường tròn (C) : (x − 1)2 + (y + 2)2 = 25 và đường thẳng d : x + 2y − 10 = 0. Tìm điểm M trên d sao cho: (a) Đường thẳng qua M, vuông góc với d là tiếp tuyến của (C). (b) Hai tiếp tuyến với (C) qua M tạo với nhau một góc vuông. (c) Tam giác tạo bởi M và hai tiếp điểm của các tiếp tuyến với (C) qua M là tam giác đều. (d) Hai tiếp tuyến với (C) qua M tạo với nhau một góc lớn nhất.
Cho ( C ) : y = x 3 - 3 x 2 + ( m - 2 ) x Biết tiếp tuyến của (C) có hệ số góc nhỏ nhất vuông góc với đường thẳng d: x-y+1=0. Khi đó giá trị của m bằng
A. 1
B. 2
C. 4
D. -5
Mọi người giúp e ý 2 vs 3 vs ạ . E cảm ơn mọi người nhiều 💛 Cho (C):y= x+3\x-1 viết phương trình pháp tuyến của(C) biết:
2. Tiếp tuyến song song với đường thẳng d: x+y+2=0
3. Tiếp tuyến vuông góc với đường thẳngd’: 4x-y+1=0
Chắc đề yêu cầu viết pt tiếp tuyến?
\(y=\frac{x+3}{x-1}\Rightarrow y'=\frac{-4}{\left(x-1\right)^2}\)
a/ Do tiếp tuyến song song với \(x+y+2=0\Leftrightarrow y=-x-2\) nên có hệ số góc bằng -1
\(\Rightarrow\frac{-4}{\left(x_0-1\right)^2}=-1\Rightarrow\left(x_0-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x_0=5\Rightarrow y_0=2\\x_0=-3\Rightarrow y_0=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-1\left(x-5\right)+2\\y=-1\left(x+3\right)+0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=-x+7\\y=-x-3\end{matrix}\right.\)
b/ \(4x-y+1=0\Leftrightarrow y=4x+1\)
Do tiếp tuyến vuông góc với d' nên
\(-\frac{4}{\left(x_0-1\right)^2}.\left(4\right)=-1\Leftrightarrow\left(x_0-1\right)^2=16\Rightarrow\left[{}\begin{matrix}x_0=17\Rightarrow y_0=\frac{5}{4}\\x_0=-15\Rightarrow y_0=\frac{3}{4}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-\frac{1}{4}\left(x-17\right)+\frac{5}{4}\\y=-\frac{1}{4}\left(x+15\right)+\frac{3}{4}\end{matrix}\right.\)
Bạn tự rút gọn nhé