Cho các đường thẳng d 1 : x - 1 1 = y + 1 2 = z - 1 và d 2 : x - 2 1 = y 2 = z + 3 2 . Viết phương trình đường thẳng D đi qua A (1; 0; 2), cắt d1 và vuông góc với d2.
![]()
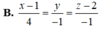
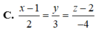
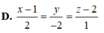
Cho đường thẳng (d): y=(m+2)x-m2 (m là tham số) .Tìm m để đường thẳng (d) và các đường thẳng y=x-1 ; x-2y=3 cắt nhau tại 1 điểm.
Ta có: y=x-1
nên x-1=y
=>x-y=1
Tọa độ giao điểm của hai đường x-y=1 và x-2y=3 là:
\(\left\{{}\begin{matrix}x-y=1\\x-2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Thay x=-1 và y=-2 vào y=(m+2)x-m2, ta được:
\(-m^2+\left(-1\right)\cdot\left(m+2\right)=-2\)
\(\Leftrightarrow-m^2-m-2=-2\)
\(\Leftrightarrow m^2+m=0\)
=>m=0 hoặc m=-1
`x-2y=3<=>y=1/2x-3/2`
Xét hệ ptr:`{(y=x-1),(y=1/2x-3/2):}`
`<=>{(1/2x+1/2=0<=>x=-1),(y=-1-1=-2):}`
Để `(d)` cắt các đường thẳng `y=x-1` và `x-2y=3` tại `1` điểm thì `3` đường thẳng này phải đồng quy
Tức là: `x=-1;y=-2` thuộc `(d)`
`=>-2=(m+2).(-1)-m^2`
`<=>m^2+m=0`
`<=>m(m+1)=0`
`<=>m=0` hoặc `m=-1`
Vậy `m={0;-1}`
cho đường thẳng (d):y=(m+2)x-m^2(m là tham số).tìm m để đường thẳng (d) và các đường thẳng y=x-1;x=2y=3 cắt nhau tại 1 điểm
Sửa đề: x+2y=3
Tọa độ giao là:
x-y=1 và x+2y=3
=>x=5/3 và y=2/3
Thay x=5/3 và y=2/3 vào (d), ta được"
5/3(m+2)-m^2=2/3
=>5/3m+10/3-m^2-2/3=0
=>-m^2+5/3m+8/3=0
=>-3m^2+5m+8=0
=>-3m^2+8m-3m+8=0
=>(3m-8)(-m-1)=0
=>m=-1 hoặc m=8/3
Cho các hàm 1 số bậc nhất y = (m - 1)x + m - 1 có c dỗ thị là đường thăng (d) và y=-x+1 có đồ thị là đường thẳng (d)
a) Với m = 2, tìm tọa độ giao điểm của hai đường thẳng (d) và (d).
b) Tìm tất tất cả các giá trị của m để đường thẳng (d) đi qua điểm A(3; 4).
c) Tìm tất cả các giá trị của m để đường thẳng (d) cắt đường thẳng (d).
a: Thay m=2 vào y=(m-1)x+m-1, ta được:
y=(2-1)x+2-1=x+1
Phương trình hoành độ giao điểm là:
x+1=-x+1
=>2x=0
=>x=0
Thay x=0 vào y=x+1, ta được:
y=0+1=1
Vậy: Tọa độ giao điểm là A(0;1)
b: Thay x=3 và y=4 vào y=(m-1)x+m-1, ta được;
3(m-1)+m-1=4
=>4(m-1)=4
=>m-1=1
=>m=2
c: Để hai đường thẳng này cắt nhau thì \(m-1\ne-1\)
=>\(m\ne0\)
Trong không gian Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 - t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d, d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x - 1 - 2 = y - 2 1 = z 3
B. x - 4 - 2 = y - 1 = z - 2 3
C. x 2 = y - 3 - 1 = z + 1 - 3
D. x - 2 - 2 = y - 1 1 = z - 1 3
Cho đường thẳng d : x - 1 2 = y + 1 - 1 = z 1 và các điểm A(1;-1;2), B(2;-1;0). Tìm tọa độ điểm M thuộc đường thẳng d sao cho tam giác AMB vuông tại M
![]()
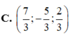
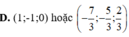
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 - t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d, d' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x - 1 - 2 = y - 2 1 = z 3
B. x - 4 - 2 = y - 1 = z - 2 3
C. x 2 = y - 3 - 1 = z + 1 - 3
D. x - 2 - 2 = y - 1 1 = z - 1 3
Đáp án D
HD: Để AB nhỏ nhất <=> AB là đoạn vuông góc chung của d, d'
Gọi A ∈ d => A(1+a;2-a;a) và B ∈ d => B(2b,1+b;2+b) ⇒ A B → = ( 2 b - a - 1 ; a + b - 1 ; b - a + 2 )
Vì A B ⊥ d A B ⊥ d ' ⇒ A B → . u d → A B → . u d ' → ⇔ 2 b - a - 1 - a - b + 1 + b - a + 2 = 0 2 ( 2 b - a - 1 ) + a + b - 1 + b - a + 2 = 0
⇔ - 3 a + 2 b + 2 = 0 - 2 a + 6 b - 1 = 0 ⇔ a = 1 b = 1 2
Vậy A(2;1;1), B 1 ; 3 2 ; 5 2 ⇒ A B → = - 1 ; 1 2 ; 3 2 = - 1 2 2 ; - 1 ; - 3
⇒ ( A B ) : x - 2 - 2 = y - 1 1 = z - 1 3
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x = 1 + t y = 2 − t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d , d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x − 1 − 2 = y − 2 1 = z 3 .
B. x − 4 − 2 = y − 1 = z − 2 3 .
C. x 2 = y − 3 − 1 = z + 1 − 3 .
D. x − 2 − 2 = y − 1 1 = z − 1 3 .
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2
Đáp án C
Ta có ∆ : x = a + 5 t ' y = 1 - 12 t ' t ' ∈ ℝ z = - 5 - t ' ⇒ giải hệ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇔ 6 + t = a + 15 t ' - 2 - 5 t = 1 - 12 t ' - 1 + t = - 5 - t ' ⇒ a = 8
Cho điểm A(1; 1) và hai đường thẳng ( d 1 ): y = x − 1; ( d 2 ): y = 4x − 2. Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d1), ( d 1 ) tạo thành một tam giác vuông.
A. y = 2x–1
B. y = –2x+3
C. y = − x + 2 y = − 1 4 x + 5 4
D. Không xác định được
Cho đường thẳng (d): y=ax+b
a) Tìm a,b sao cho (d) đi qua A(1;-1) và song song với đường thẳng y=2x+3
b) Vẽ đường thẳng (d)
c) Tìm m sao cho 3 đường thẳng (d) và y=x+1 và y=(m-1).x+5 đồng qui.
a: Vì (d)//y=2x+3 nên a=2
Vậy: (d): y=2x+b
Thay x=1 và y=-1 vào (d), ta được:
b+2=-1
hay b=-3
c. Gọi: \(\left[{}\begin{matrix}y=x+1\left(d'\right)\\y=\left(m-1\right)x+5\left(d''\right)\end{matrix}\right.\)
Ta có: \(PTHDGD:\left(d\right)-\left(d'\right)\)
\(2x+3=x+1\)
\(\Rightarrow x=-2\left(1\right)\)
\(Thay\left(1\right)in\left(d'\right):y=-2+1=-1\)
\(\Rightarrow A\left(-2;-1\right)\)
Để 3 đt này đồng quy, thì \(A\left(-2;-1\right)\in\left(d''\right)\Leftrightarrow-1=-2m+2+5\)
\(\Rightarrow m=4\)