chứng minh
a.[b-c]-b.[a-c]bằng c.[b-a]
Những câu hỏi liên quan
cho a/b = c/d chứng minh
a] a/a-b=c/c-d
b] a/b=a+c/b+d
c] a/3a+b=c/3c+d
Cho mình cách giải cảm ơn mn
a: \(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\)
Đúng 0
Bình luận (0)
cho tỷ lệ thức a/c=c/b (a,b,c khác 0). Chứng minh
a) a2+c2/b2+c2=a/b
b) b2-a2 / a2+c2= b-a/a
\(a,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow\dfrac{a^2}{c^2}=\dfrac{c^2}{b^2}=\dfrac{a^2+c^2}{b^2+c^2}\left(1\right)\)
Mà \(\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\Leftrightarrow\dfrac{a}{b}=\dfrac{c^2}{b^2}\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\tođpcm\)
\(b,\dfrac{a}{c}=\dfrac{c}{b}\Leftrightarrow ab=c^2\)
\(\Leftrightarrow\dfrac{b^2-a^2}{a^2+c^2}=\dfrac{\left(b-a\right)\left(b+a\right)}{a^2+ab}=\dfrac{\left(b-a\right)\left(b+a\right)}{a\left(a+b\right)}=\dfrac{b-a}{a}\left(đpcm\right)\)
Đúng 3
Bình luận (0)
Cho a,b,c >0 thỏa mãn a+b+c\(\le\)\(\frac{3}{2}\).Chứng minh
a,\(\frac{1}{a}\)+\(\frac{1}{b}\)+\(\frac{1}{c}\)\(\ge\)6
b,a+ b+ c+ \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)\(\ge\)\(\frac{15}{2}\)
a)Áp dụng BĐT cosi-schwart:
`A=1/a+1/b+1/c>=9/(a+b+c)`
Mà `a+b+c<=3/2`
`=>A>=9:3/2=6`
Dấu "=" `<=>a=b=c=1/2`
b)Áp dụng BĐT cosi:
`a+1/(4a)>=1`
`b+1/(4b)>=1`
`c+1/(4c)>=1`
`=>a+b+c+1/(4a)+1/(4b)+1/(4c)>=3`
Ta có:
`1/a+1/b+1/c>=6`(Ở câu a)
`=>3/4(1/a+1/b+1/c)>=9/2`
`=>a+b+c+1/(a)+1/(b)+1/(c)>=3+9/2=15/2`
Dấu "=" `<=>a=b=c=1/2`
Đúng 2
Bình luận (0)
a)Áp dụng BĐT cosi-schwart:
A=1a+1b+1c≥9a+b+cA=1a+1b+1c≥9a+b+c
Mà a+b+c≤32a+b+c≤32
⇒A≥9:32=6⇒A≥9:32=6
Dấu "=" ⇔a=b=c=12⇔a=b=c=12
b)Áp dụng BĐT cosi:
a+14a≥1a+14a≥1
b+14b≥1b+14b≥1
c+14c≥1c+14c≥1
⇒a+b+c+14a+14b+14c≥3⇒a+b+c+14a+14b+14c≥3
Ta có:
1a+1b+1c≥61a+1b+1c≥6(Ở câu a)
⇒34(1a+1b+1c)≥92⇒34(1a+1b+1c)≥92
⇒a+b+c+1a+1b+1c≥3+92=152⇒a+b+c+1a+1b+1c≥3+92=152
Dấu "=" ⇔a=b=c=12
Đúng 0
Bình luận (0)
Cho A=a+b-5
B=b-c+1
C=b-c-4
D=b-a
Chứng minhA+B=C-D
Ta có
A + B = ( a + b - 5 ) + ( -b - c +1 ) = a + b - 5 -b - c + 1 = a- c -4
C - D = ( b - c - 4 ) - ( b - c ) = b - c - 4 + a = a - c - 4
Vậy A+D = C- D
Đúng 0
Bình luận (0)
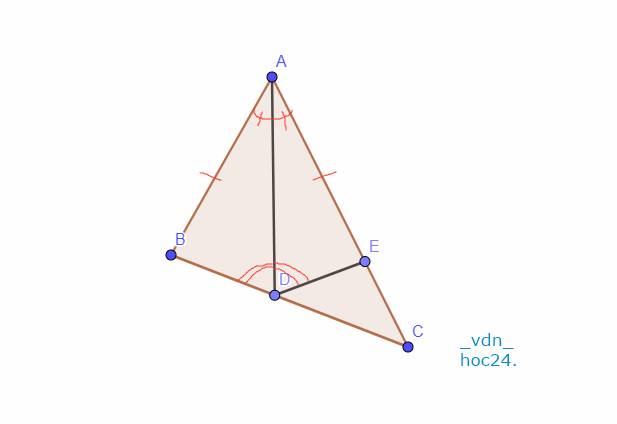
Cho tam giác ABC có AB < AC . Phân giác của góc A cắt cạnh BC tại điểm D. Trên cạnh AC lấy điểm E sao cho AE = AB. Chứng minh
a) ∆ A B D = ∆ A E D .
b) DA là tia phân giác của góc BDE. Từ đó suy ra A B C ^ > A C B ^ .
\(\text{#TNam}\)
`a,` \(\text{Xét Tam giác ABD và Tam giác AED có:}\)
`AB = AE (g``t)`
\(\widehat{BAD}=\widehat{EAD} (\text {tia phân giác} \) \(\widehat{BAE})\)
`\text {AD chung}`
`=> \text {Tam giác ABD = Tam giác AED (c-g-c)}`
`b,`
\(\text{Vì Tam giác ABD = Tam giác AED (a)}\)
`->`\(\widehat{ADB}=\widehat{ADE} (\text {2 góc tương ứng})\)
`-> \text {AD là tia phân giác}` \(\widehat{BDE}\)
\(\text{Xét Tam giác ABC:}\)
`AC > AB (g``t)`
\(\text{Theo định lý của quan hệ giữa góc và cạnh đối diện trong 1 tam giác}\)
`->`\(\widehat{ABC}>\widehat{ACB}.\)
Đúng 2
Bình luận (0)
Gọi O là điểm bất kì nằm trong △ABC.A1,B1,C1 lần lượt là TĐ OA,OB,OC .A',B',C' lần lượt là TĐ B1C1,A1C1,A1B1.Chứng minh
a.△ABC đồng dạng △A'B'C'
b.Góc ABC=Góc A'B'C'
Giúp mik với ạ!!!
Cho ba điểm A, B, C thẳng hàng (điểm B nằm giữa A và C). Đường tròn (O) đi qua B và C, đường kính DE vuông góc với BC tại K. AD cắt (O) tại F; EF cắt AC tại I. Chứng minh
a) Tứ giác DFIK nội tiếp.Xác định tâm của đường tròn ngoại tiếp tứ giác DFIK
b) \(\widehat{DEA}=\widehat{DIK}\)
c) AI . KE . KD = KI . AB . AE
Cho nửa đường tròn đường kính AB. Trên nửa đường tròn lấy C (C khác A, B). Gọi H là hình chiếu của C trên AB. Trên cung CB lấy D (D khác C, B). Hai đường thẳng AD và CH cắt tại E Chứng minh
a) tứ giác BDEH nội tiếp.
b )Chứng minh AC^2 = AE.AD
c ) gọi (O) là đường tròn qua D và tiếp xúc AB tại B ,(O') cắt CB tại F.Chứng minh EF//AB
a) ta có góc ADB = 90 độ (góc nội tiếp chắn nửa đường tròn)
tứ giác BDEH có: góc EHB+ góc EDB = 90+90=180 độ
=> tứ giác BDEH nội tiếp
b) tứ giác ACDB nội tiếp ( do có 4 đỉnh nằm trên đường tròn)
=> góc ACD+góc DBA =180 độ
ta lại có góc HED+gócDBA=180 độ ( tứ giác DBHE nội tiếp)
=>góc ACD= gócHED
mà góc HED=gócAEC (đối đỉnh)
=> góc ACD=góc AEC
xét hai tam giác ACE và ADC có góc CAD chung ; góc ACD=gócAEC
=> △ACE đồng dạng △ADC(góc - góc)
=> \(\dfrac{AC}{AD}=\dfrac{AE}{AC}\)=>AC2=AD*AE
Đúng 0
Bình luận (0)
Cho hai đường thẳng xy và mn cắt nhau tại O. Trên Ox; Oy; Om; On lần lượt lấy 4 điểm A;B;C;D sao cho OA=OB; OC=OD. Chứng minh
a/Tam giác ODA bằng tam giác OCB
b/AD=BC
c/BD// AC
a: Xét ΔODA và ΔOCB có
OD=OC
góc DOA=góc COB
OA=OB
Do đó: ΔODA=ΔOCB
b: Xét tứ giác ADBC có
O là trung điểm chung của AB và DC
nên ADBC là hình bình hành
=>AD=BC
c: ADBC là hình bình hành
=>AC//BD
Đúng 0
Bình luận (0)