Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài
Pham Trong Bach
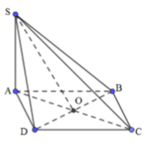
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc B A C ^ 60 0 . Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Mặt phẳng (SAC) hợp với mặt phẳng (ABCD) một góc 450. Thể tích khối chóp S.ABCD bằng:
Đọc tiếp
Lớp 12 Toán
Những câu hỏi liên quan
Pham Trong Bach
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAC ^ 60 ° ,   SO ⊥ ( ABCD ) và SO 3a/4. Tính thể tích khối chóp S.ABCD. A. a 3 3 8 B. a 3...
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
23 tháng 10 2018 lúc 5:23

Đáp án A

Bình luận (0)
Hà Thị Ngọc Dung

cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với mặt phẳng đáy, SA=BD=a√3. Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng

A. 60°  B. 30°  C.90°  D.45°

 

Xem chi tiết
Lớp 12 Toán Câu hỏi của OLM

Khách
 
Lê Song Phương
Lê Song Phương
16 tháng 6 2023 lúc 10:14

 Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).

Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A. 

Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A

 

Bình luận (0)
Lê Song Phương
Lê Song Phương
16 tháng 6 2023 lúc 10:15

Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.

Bình luận (0)
Pham Trong Bach

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 °  cạnh bên SA = a 2  và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).

A. 90 °

B. 30 °

C. 45 °

D. 60 °

Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
16 tháng 6 2017 lúc 11:23

Chọn B.

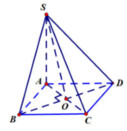
Gọi O = AC ∩ BD. Vì ABCD là hình thoi nên BO ⊥ AC(1). Lại do:

Từ (1) và (2) ta có:BO ⊥ (SAC)

Ta có: 

Vì ABCD là hình thoi có ABC = 60 ° nên tam giác ABC đều cạnh a

Trong tam giác vuông SBO ta có: 

Bình luận (0)
Pham Trong Bach
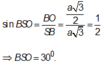
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc  A B C ^ 60 °  . Biết SA SB SC a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng: A.  60 °   B.  30 °   C.  45 °   D.  90 °  
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
6 tháng 1 2019 lúc 17:00

Chọn D.

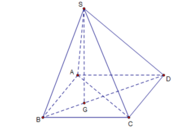
Đề thi Học kì 2 Toán 11 có đáp án (Đề 1)

- Gọi G là trọng tâm tam giác ABC.

- Hình chóp S.ABC là hình chóp đều nên SG ⊥ (ABC).

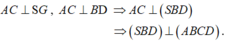
Đề thi Học kì 2 Toán 11 có đáp án (Đề 1)

→ Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng  90 °  

Bình luận (0)
Lê vsbzhsjskskskssm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAD = 60 ° với AC cắt BD tại O, SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.

Xem chi tiết
Lớp 11 Toán

Khách
 
Akai Haruma
Akai Haruma Giáo viên
8 tháng 6 2021 lúc 21:36

Lời giải:

$\widehat{BAD}=60^0\Rightarrow \widehat{BAO}=30^0$

$\frac{BO}{AB}=\sin \widehat{BAO}=\sin 30^0=\frac{1}{2}$

$\Rightarrow BO=\frac{AB}{2}=\frac{a}{2}$

$BD=2BO=a$

$\frac{AO}{AB}=\cos \widehat{BAO}=\cos 30^0=\frac{\sqrt{3}}{2}$

$\Rightarrow AO=\frac{\sqrt{3}a}{2}$

$\Rightarrow AC=\sqrt{3}a$

$S_{ABCD}=\frac{BD.AC}{2}=\frac{\sqrt{3}a^2}{2}$

$V_{S.ABCD}=\frac{1}{3}.SO.S_{ABCD}=\frac{1}{3}.\frac{3a}{4}.\frac{\sqrt{3}a^2}{2}=\frac{\sqrt{3}a^3}{8}$

Bình luận (0)
Pham Trong Bach
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, D ^ 60° và SA vuông góc với (ABCD). Biết thể tích của khối chóp S.ABCD bằng a 3 2 . Tính khoảng cách k từ A đến mặt phẳng (SBC). A. k 3 a 5 B.  k a...
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
17 tháng 8 2017 lúc 6:37

Đáp án B

Bình luận (0)
Nguyễn Thùy Chi

Cho hình chóp S.ABCD có mặt phẳng đáy hình thoi cạnh a, ABC =60°, SA vuông góc mặt phẳng đáy là SA=\(a\sqrt{3}\). Tính góc giữa (SBC) và (ABCD) ?

 
Xem chi tiết
Lớp 11 Toán Bài 6: Ôn tập chương Vecơ trong không gian. Quan h...

Khách
 
Dao Nguyen

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC=60°. Cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với mặt đáy một góc 60°. Gọi I là trung điểm BC, H là hình chiếu vuông góc của A lên SI. Tính thể tích khối chóp S.ABCD và khoảng cách từ điểm H đến (SCD) theo a.

Xem chi tiết
Lớp 12 Toán Chương 1: KHỐI ĐA DIỆN

Khách
 
Nguyễn Hoàng Việt
Nguyễn Hoàng Việt
18 tháng 12 2016 lúc 17:34

a) Dễ dàng chứng minh tam giác ABC và ACD đều

Suy ra AC=a, SA= AC.tan(gócSCA)=a.tan(600)

\(V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.a\sqrt{3}.a^2.\frac{\sqrt{3}}{2}=\frac{a^3}{2}\)

b) Có 2 cách làm để tìm khoảng cách từ H đến mp(SCD), nhưng bạn nên chọn phương pháp tọa độ hóa cho dễ

Chọn A làm gốc tọa độ , các tia AD, AI, AS lần lượt trùng tia Ax, Ay, Az

Có ngay tọa độ các điểm \(S\left(0;0;a\sqrt{3}\right)\) , \(D\left(a;0;0\right)\) , \(I\left(0;\frac{a\sqrt{3}}{2};0\right)\)

\(\Rightarrow C\left(\frac{a}{2};\frac{a\sqrt{3}}{2};0\right)\)

theo số liệu đã cho, dễ xác định được điểm H chia đoạn SI với tỷ lệ 2:1

\(\Rightarrow H\left(0;\frac{a}{\sqrt{3}};\frac{a}{\sqrt{3}}\right)\)

Bây giờ chỉ cần viết pt (SCD) là tính được ngay khoảng cách từ H đến SCD

\(\left(SCD\right):\sqrt{3}x+y+z-\sqrt{3}=0\)

\(d\left(H\text{/}\left(SCD\right)\right)=\frac{a\sqrt{3}}{\sqrt{5}}\)

Bình luận (5)
Pham Trong Bach
Cho khối chóp S.ABCD có đáy ABCD là hình thoi cạnh a góc ABC 60 ° , chiều cao bằng 3a thể tích của khối chóp bằng.  A. a 3 2 3 B.  3 a 2 3 C.  2 a 3 12 D. ...
Đọc tiếp
Xem chi tiết
Lớp 0 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
28 tháng 12 2017 lúc 13:30

Chọn D

Bình luận (0)
Pham Trong Bach
Cho hình chóp  S.ABCD  có đáy là hình thoi cạnh 2a , góc ABC 60 0 , SA a 3  và   SA ⊥ (ABCD). Tính góc giữa SA và mặt phẳng (SBD) A. 600 B. 900  C. 300 D. 450
Đọc tiếp
Xem chi tiết
Lớp 11 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
5 tháng 4 2019 lúc 6:15

Chọn C

Phương pháp

 

Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).

 

Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.

Bình luận (0)