Cho phương trình
8 z 2 - 4 a + 1 z + 4 a + 1 = 0
với a là tham số. Tìm a ∈ ℝ để phương trình có hai nghiệm z 1 ; z 2 thỏa mãn z 1 z 2 là số ảo, trong đó z 2 là số phức có phần ảo dương.
A. a = 0
B. a = 2
C. a ∈ 0 ; 2
D. a ∈ 0 ; 1 ; 2
Những câu hỏi liên quan
28 tháng 1 2023 lúc 12:30
cho x, y, z là nghiệm bất phương trình \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\xy+yz+zx=4\end{matrix}\right.\)
Chứng minh rằng \(-\dfrac{8}{3}\) ≤ x, y, z ≤ \(\dfrac{8}{3}\)
\(X+Y+Z+8=2\sqrt{X-1}+4\sqrt{Y-2}+6\sqrt{Z-3}\)
CHO BỐ (A,B,C)THOẢI MÃN PHƯƠNG TRÌNH TRÊN
VAY A*B-C=?
Bài này không thể giải được vì không có dữ kiện gì về A, B, C cả, bên trên X, Y, Z còn bên dưới A, B, C thì sao mà giải
Đúng 0
Bình luận (0)
19 tháng 1 lúc 11:56
Giải phương trình:
\(\left(\dfrac{z^2+2z+4}{z-2}\right)^2+7=\dfrac{8-z^3}{\left(z-2\right)^2}\)
ĐKXĐ: \(z\ne2\)
\(\left(\dfrac{z^2+2z+4}{z-2}\right)^2+7+\dfrac{\left(z-2\right)\left(z^2+2x+4\right)}{\left(z-2\right)^2}=0\)
\(\Leftrightarrow\left(\dfrac{z^2+2z+4}{z-2}\right)^2+\dfrac{z^2-2z+4}{z-2}+7=0\)
Đặt \(\dfrac{z^2+2z+4}{z-2}=x\)
\(\Rightarrow x^2+x+7=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{27}{4}=0\)
Pt đã cho vô nghiệm
Đúng 2
Bình luận (1)
bài 1 giải phương trình
a) \(\frac{x+5}{x-1}=\frac{x+1}{x-3}-\frac{8}{x^2-4x+3}\)
B) \(\frac{2}{\left(1-3x\right)\left(3x+11\right)}=\frac{1}{9x^2-6x+1}-\frac{3}{\left(3x+11\right)^2}\)
Bài 2 cho ẩn z
\(\frac{z}{3z+z}-\frac{z}{z-3a}=\frac{a^2}{9a^2-z^2}\)
a) giải phương trình khi a=1
b) tìm cá giá trị a khi z=1
Phương trình phóng xạ: \(^{_{17}^{35}Cl}+^{_Z^A}X\rightarrow n+^{37}_{18}Ar\) Trong đó Z,A là
A. Z=1; A=1
B. Z=1; A=3
C. Z=2; A=3
D. Z=2; A=4
\(^{35}_{17}Cl+^A_ZX\rightarrow n+^{37}_{18}Ar\)
Ta có:
\(\left\{{}\begin{matrix}35+A=1+37\\17+Z=0+18\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}A=3\\Z=1\end{matrix}\right.\)
Chọn B
Đúng 2
Bình luận (0)
Trong không gian Oxyz, cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là
x
-
3
-
1
y
-
3
2
z
-
2
-
1
, phương trình đường phân giác trong...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có A (2;3;3), phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng BC có một vectơ chỉ phương là:
A . u → = 2 ; 1 ; - 1
B . u → = 1 ; 1 ; 0
C . u → = 1 ; - 1 ; 0
D . u → = 1 ; 2 ; 1
Chọn C
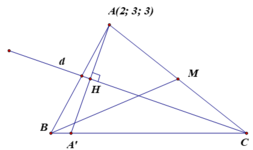
Gọi M là trung điểm của AC. Khi đó M thuộc vào đường trung tuyến kẻ từ B của tam giác ABC.
Giả sử M (3 – t ; 3 + 2t ; 2 – t) ∈ Δ suy ra C (4-2t; 3+4t; 1-2t).
Mà C thuộc và đường phân giác trong d của góc C nên ta có: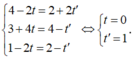 
Suy ra C (4; 3; 1).
Gọi H là hình chiếu vuông góc của A trên đường phân giác trong d.
Suy ra H (2+2t';4-t';2-t') 
Ta có 
ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
=> H (2;4;2).
Gọi A' đối xứng với A qua đường phân giác trong d.
Suy ra A’ ∈ (BC) và A' (2;5;1). Khi đó 
là vectơ chỉ phương của đường thẳng BC.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3), phương trình đường trung tuyến kẻ từ B là
x
-
3
-
1
y
-
3
2
z
-
2
-
1
, phương trình đường phân giác trong c...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3), phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng BC có một vectơ chỉ phương là
A. u → = 2 ; 1 ; - 1
B. u → = 1 ; 1 ; 0
C. u → = 1 ; - 1 ; 0
D. u → = 1 ; 2 ; 1
Trong không gian Oxyz, cho tam giác ABC có A ( 2;3;3) phương trình đường trung tuyến kẻ từ B là
x
−
3
−
1
y
−
3
2
z
−
2
−
1
,
phương trình đường phân giá...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có A ( 2;3;3) phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Đường thẳng AB có vecto chỉ phương là :
A. u 3 → 2 ; 1 ; − 2
B. u 2 → 1 ; − 1 ; 0
C. u 4 → 0 ; 1 ; − 1
D. u 1 → 1 ; 2 ; 1
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3) phương trình đường trung tuyến kẻ từ B là
x
-
3
-
1
y
-
3
2...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3) phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng AB có vecto chỉ phương là :
A. (2;1;-2)
B. (1;-1;0)
C. (0;1;-1)
D. (1;2;1)
Đáp án C
Phương pháp:
+) Tam giác ABC có trung tuyến BM và phân giác CD.
+) Tham số hóa tọa độ điểm M là trung điểm của AC, tìm tọa độ điểm C theo tọa độ điểm M.
+) Tìm tọa độ điểm N đối xứng với M qua CD =>N ∈ BC => Phương trình đường thẳng BC
+) Tìm tọa độ điểm B=BM ∩ BC, khi đó mọi vector cùng phương với AB đều là VTCP của AB.
Cách giải:
Tam giác ABC có trung tuyến BM và phân giác CD.
Gọi M(30t; 3+2t;2-t) ∈ BM là trung điểm của AC ta có
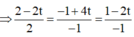
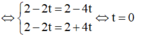
Gọi H là hình chiếu của M trên CD ta có
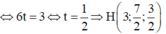
Gọi N là điểm đối xứng với M qua CD => H là trung điểm của MN
Do CD là phân giác của góc C nên N ∈ BC, do đó phương trình đường thẳng CB là
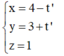
Xét hệ phương trình
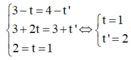
=> B(2;5;1)
Đúng 0
Bình luận (0)
Cho phương trình
z
3
+
a
z
2
+
b
z
+
c
0
Nếu z1-i và z1 là 2 nghiệm của phương trình thì
a
-
b
-
c
bằng A. 2 B. 3 C. 5 D. 6
Đọc tiếp
Cho phương trình z 3 + a z 2 + b z + c = 0 Nếu z=1-i và z=1 là 2 nghiệm của phương trình thì a - b - c bằng
A. 2
B. 3
C. 5
D. 6
