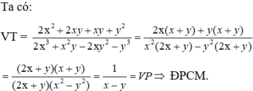ko trả lời thì thôi đừng nhắn bậy

đúng ko trả lời cứ nhắn bậy

M=(x3+x2y-2x2)+(2y-y2-xy)+(x+y-2)+2020

M=x2(x+y-2)+y(2-y-x)+(x+y-2)+2020

M=x2.0+y.0+0+2020

M=2020

Vậy M=2020

không hiểu chỗ nào hỏi mình nha!

\(M=x^3+x^2y-2x^2-xy-y^2+3y+x+2017\)

\(\Rightarrow M=\left(x^3+x^2y-2x^2\right)-xy-y^2+2y+y+x-2+2019\)

\(\Rightarrow M=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+\left(y+x-2\right)+2019\)

\(\Rightarrow M=x^2\left(x+y-2\right)-y\left(x+y-2\right)+\left(x+y-2\right)+2019\)

\(\Rightarrow M=\left(x^2-y+1\right)\left(x+y-2\right)+2019\)

\(\Rightarrow M=\left(x^2-y+1\right).0+2019\)

\(\Rightarrow M=0+2019\)

\(\Rightarrow M=2019\)

Đáp án: A

M = x³ + x²y - 2x² - xy - y² + 3y + x + 2017

M = (x³ + x²y - 2x²) - (xy + y² - 2y) + (x + y - 2) + 2019

M = x². (x + y - 2) - y(x + y - 2) + (x + y - 2) + 2019 = 2019

\(M = x^3 + x^2y - 2x^2 - xy - y^2 + 3y + x + 2017.\)

\(M=(x^3+x^2y-2x^2)-(xy-y^2+2y)+(x+y-2)+2019\)

\(M=x^2.(x+y-2)-y.(x-y+2)+(x+y-2)+2019\)

\(M=x^2.0-y.0+0+2019\)

\(M=0-0+0+2019\)

\(M=2019\)

$M={}^{}+{}^{}y-2{}^{}-xy-{}^{}+3y+x+2017.$

$M=({}^{}+{}^{}y-2{}^{})-(xy-{}^{}+2y)+(x+y-2)+2019$

$M={}^{}.(x+y-2)-y.(x-y+2)+(x+y-2)+2019$

$M={}^{}.0-y.0+0+2019$

\(A=x^3+x^2y-2x^2-xy-y^2+3y+x+2019\)

\(=x^3+x^2\left(2-x\right)-2x^2-y\left(x+y\right)+3y+x+2019\)

\(=x^3+2x^2-x^3-2x^2-2y+3y+x+2019\)

\(=x+y+2019=2021\)

1q

Lời giải:

PT $\Leftrightarrow x^3+x+1-y(x^2-3)=0$

$\Leftrightarrow y=\frac{x^3+x+1}{x^2-3}$ (hiển nhiên $x^2-3\neq 0$ với mọi $x$ nguyên) 

Để $y$ nguyên thì $\frac{x^3+x+1}{x^2-3}$ nguyên 

$\Leftrightarrow x^3+x+1\vdots x^2-3$
$\Rightarrow x(x^2-3)+4x+1\vdots x^2-3$
$\Rightarrow 4x+1\vdots x^2-3$

Hiển nhiên $4x+1\neq 0$ nên $|4x+1|\geq x^2-3$
Nếu $x\geq \frac{-1}{4}$ thì $4x+1\geq x^2-3$
$\Leftrightarrow x^2-4x-4\leq 0$

$\Leftrightarrow (x-2)^2\leq 8<9$

$\Rightarrow -3< x-2< 3$

$\Rightarrow -1< x< 5$

$\Rightarrow x\in \left\{0; 1; 2; 3; 4\right\}$.

Nếu $x< \frac{-1}{4}$ thì $-4x-1\geq x^2-3$

$\Leftrightarrow x^2+4x-2\leq 0$

$\Leftrightarrow (x+2)^2-6\leq 0$

$\Leftrightarrow (x+2)^2\leq 6< 9$

$\Rightarrow -3< x+2< 3$
$\Rightarrow -5< x< 1$

$\Rightarrow x\in\left\{-4; -3; -2; -1\right\}$

Đến đây bạn thay vào tìm $y$ thôi

\(VT=\dfrac{2x^2+2xy+xy+y^2}{x^2\left(2x+y\right)-y^2\left(2x+y\right)}=\dfrac{2x\left(x+y\right)+y\left(x+y\right)}{\left(x^2-y^2\right)\left(2x+y\right)}\\ =\dfrac{\left(2x+y\right)\left(x+y\right)}{\left(2x+y\right)\left(x-y\right)\left(x+y\right)}=\dfrac{1}{x-y}=VP\)