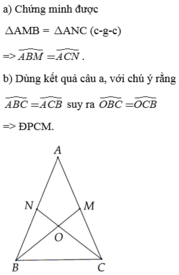
Cho tam giác ABC cân tại Ạ. Trên các cạnh AC,AB lần lượt lấy M, N sao cho AM = AN. a) Chứng minh A B M ^ = A C N ^ b) Gọi O là giao điểm của BM. và CN. Chứng minh tam giác OBC cân

Những câu hỏi liên quan
Cho tam giác ABC cân tại A. Trên các cạnh AC,AB lần lượt lấy M, N sao cho AM = AN.
a) Chứng minh A B M ^ = A C N ^
b) Gọi O là giao điểm của BM và CN. Chứng minh tam giác OBC cân.
Cho tam giác ABC cân tại A, trên cạnh AB và AC lần lượt lấy hai điểm M và N, sao cho AM = AN. Chứng minh rằng: Góc ABN = Góc ACM.
Xét ΔABN và ΔACM có
AB=AC
\(\widehat{A}\) chung
AN=AM
Do đó: ΔABN=ΔACM
Suy ra: \(\widehat{ABN}=\widehat{ACM}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Trên cạnh AB và Ac lần lượt lấy 2 điểm M và N sao cho AM =AN , chứng minh tứ giác MNCB là hình thang
Cho tam giác ABC cân tại A. Trên AB ,AC lần lượt lấy M , N sao cho AM = AN a) chứng minh MNCB là hình thang cân b) cho góc A = 55° . Tính các góc của hình thang cân đó
a: Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
Do đó: MN//BC
Xét tứ giác MNCB có MN//BC
nên MNCB là hình thang
mà \(\widehat{C}=\widehat{B}\)
nên MNCB là hình thang cân
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Trên các cạnh AC, AB lần lượt lấy M, N sao cho AM = AN.
a) Chứng minh BN=CM
b) Gọi O là giao điểm của BM và CN. Chứng minh tam giác OBC cân.
a: AM+MC=AC
NA+NB=AB
mà AB=AC; AM=AN
nên MC=NB
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc OBC=góc OCB
=>ΔOBC cân tại O
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. TRên các cạnh AB ; AC lần lượt lấy các điểm M và N sao cho AM + AN = AB. CHứng minh rằng: Khi M và N di chuyển trên AB và AC nhưng vẫn thỏa mãn AM + AN = AB thì đường trung trực của MN luôn đi qua một điểm cố định
. Cho tam giác ABC cân tại A. Trên các cạnh AC, AB lần lượt lấy M, N sao cho AM = AN.
a) Chứng minh tam giác ABM = tam giác ACN .
b) Chứng minh MN // BC.
c) Gọi O là giao điểm của BM và CN. Chứng minh tam giác OBC cân.
a) Xét tam giác ABM và tam giác ACN:
Góc A chung
AB = AC (do tam giác ABC cân tại A)
AM = AN (gt)
Suy ra: tam giác ABM = tam giác ACN (c g c)
Đúng 1
Bình luận (0)
b) Xét tam giác AMN có :
AM =AN (gt)
Suy ra: tam giác AMN cân tại A
Suy ra góc ANM = \(\dfrac{\text{180 - góc A}}{2}\)
mà góc ABC = \(\dfrac{\text{180 - góc A}}{2}\) ( do tam giác ABC cân tại A)
Suy ra: góc ANM = góc ABC
Mà 2 góc này ở vị trí đồng vị của MN và BC
Suy ra MN song song BC
Đúng 2
Bình luận (0)
a) Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{BAM}\) chung
AM=AN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
b) Xét ΔAMN có AM=AN(gt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
hay \(\widehat{ANM}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAMN cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{ANM}=\widehat{ABC}\)
mà \(\widehat{ANM}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên MN//BC(Dấu hiệu nhận biết hai đường thẳng song song)
c) Ta có: ΔABM=ΔACN(cmt)
nên \(\widehat{ABM}=\widehat{ACN}\)(hai góc tương ứng)
Ta có: \(\widehat{ABM}+\widehat{CBM}=\widehat{ABC}\)(tia BM nằm giữa hai tia BA,BC)
\(\widehat{ACN}+\widehat{BCN}=\widehat{ACB}\)(tia CN nằm giữa hai tia CA,CB)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy trong ΔABC cân tại A)
và \(\widehat{ABM}=\widehat{ACN}\)(cmt)
nên \(\widehat{CBM}=\widehat{BCN}\)
hay \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A. Trên 2 cạnh AB và AC lần lượt lấy hai điểm M và N sao cho AM = AN. Kẻ AH vuông góc với BC, H ∈ BC
a. Chứng minh tam giác ABH = tam giác ACH
b. Chứng minh BN=CM
c. Nếu cho cạnh AH=8cm, AB= 10cm. Tính cạnh BC
a. xét tam giác ABH và tam giác ACH
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
BH = CH ( ABC cân, AH là đường cao cũng là trung tuyến )
Vậy tam giác ABH = tam giác ACH ( c.g.c )
b. xét tam giác vuông BNH và tam giác vuông CNH
BN = CM ( AB = AC ; AM = AN )
BH = CH
Vậy tam giác vuông BNH = tam giác vuông CNH ( cạnh huyền. cạnh góc vuông )
c. áp dụng định lý pitao vào tam giác vuông AHB:
\(AB^2=AH^2+BH^2\)
\(BH=\sqrt{10^2-8^2}=\sqrt{64}=8cm\)
=> BC = BH. 2 = 8.2 =16 cm
Chúc bạn học tốt!!!
Đúng 1
Bình luận (0)
a, Xét tam giác ABH và tam giác ACH
^AHB = ^AHC = 900
AB = AC (gt)
AH _ chung
Vậy tam giác ABH = tam giác ACH ( ch - cgv )
b, Xét tam ANB và tam giác AMC có :
^A _ chung
AM = AN(gt)
AB = AC (gt)
Vậy tam giác ANB = tam giác AMC ( c.g.c )
=> BN = CM ( 2 cạnh tương ứng )
c, Xét tam giác ABH vuông tại H, theo định lí Pytago
\(BH=\sqrt{AB^2-AH^2}=6cm\)
Xét tam giác ABC cân tại A có AH là đường cao nên đồng thời AH là đường trung tuyến
=> BC = 2BH = 12 cm
Đúng 1
Bình luận (0)
a, ΔABC cân tại A =>AB=AC và ACH=ABH
Xét ΔABH và ΔACH có:
ACH=ABH
AB=AC
AHC=AHB=900
=>ΔABH=ΔACH(cạnh huyền-góc nhọn) (đpcm)
b, Ta có AM+MB=AN+NC và AM=AN
=>MB=NC
Xét ΔBMC và ΔCNB có:
BM=NC
MBC=NCB
BC chung
=>ΔBMC=ΔCNB(c.g.c)
=>BN=CM (đpcm)
c, Xét ΔABH có: AB2=BH2+AH2 (pi-ta-go)
=>BH2=36
=>BH=6(cm)
ΔABC cân tại A có AH là đường cao
=> AH cũng là trung tuyến
=>HB=HC=BC/2
=>BC=2HB=12 (cm)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Trên tia đối của tia AB lấy điểm E sao cho AC = AE a) chứng minh tam giác ABC = tam giác ADE b) gọi M , N lần lượt là trung điểm của BC và DE , chứng minh AM = AN c) tính số đo của góc MAN
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
Đúng 0
Bình luận (0)
a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
Do đó: ΔABC=ΔADE
b: AM=ED/2
AN=BC/2
mà ED=BC
nên AM=AN
Đúng 0
Bình luận (0)