Tập các giá trị của m để phương trình 8 x + 2 . 8 1 - x - 9 m = 0 có 2 nghiệm phân biệt.
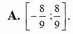
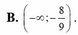
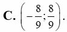
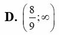
Tập các giá trị của\(m\)để 2 phương trình :\(x^2+mx+8=0\)và\(x^2+x+m=0\)có nghiệm chung.
Ta có mx +8=x+m <=> (m-1)x=m-8 <=>x=(m-8)/(m-1) điều kiện m khác 1
Cho phương trình \(x^2-\left(m-2\right)x-8=0\), với m là tham số.
Tìm tất cả các giá trị của m để phương trình có hai nghiệm \(x_1,x_2\) sao cho biểu thức \(Q=\left(x^2_1-1\right)\left(x^2_2-4\right)\) có giá trị lớn nhất.
\(\Delta=\left(m-2\right)^2+8>0\) với mọi m . Vậy pt có 2 nghiệm phân biệt với mọi m
Do : \(x_1x_2=-8\) nên \(x_2=\dfrac{-8}{x1}\)
\(Q=\left(x_1^2-1\right)\left(x_2^2-4\right)=\left(x_1^2-1\right)\left(\dfrac{64}{x_1^2}-4\right)=68-4\left(x_1^2+\dfrac{16}{x_1^2}\right)\le68-4.8=36\)
\(\left(x_1^2+\dfrac{16}{x_1^2}\ge8\right)\)\(;Q=36\) khi và chỉ khi x1 = ( 2 ; -2 )
tìm tất cả các giá trị nguyên của tham số m để bất phương trình x^2 -2.(m-1).x+4.m+8>=0 nghiệm đúng với mọi x thuộc R
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(m-1\right)^2-\left(4m+8\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow m^2-6m-7\le0\)
\(\Rightarrow-1\le m\le7\)
\(\Rightarrow m=\left\{-1;0;1;2;3;4;5;6;7\right\}\)
Câu 1 a.tìm tất cả các giá trị của tham số m để bất phương trình mx²+3mx+(m+1)>0 nghiệm đúng với mọi số thực x? b.tìm các giá trị của m để biểu thức sau luôn âm:g(x)=(m-4)x²+(2m-8)x+m-5
a: Trường hợp 1: m=0
Bất phương trình sẽ là \(0x^2+3\cdot0\cdot x+0+1>0\)
=>1>0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(3m\right)^2-4m\left(m+1\right)\)
\(=9m^2-4m^2-4m=5m^2-4m\)
Để phương trình có nghiệm đúng với mọi số thực x thì \(\left\{{}\begin{matrix}m\left(5m-4\right)< 0\\m>0\end{matrix}\right.\Leftrightarrow0< m< \dfrac{4}{5}\)
Vậy: 0<=m<4/5
b: Trường hợp 1: m=4
\(g\left(x\right)=\left(4-4\right)\cdot x^2+\left(2\cdot4-8\right)x+4-5=-1< 0\)(luôn đúng)
Trường hợp 2: m<>4
\(\text{Δ}=\left(2m-8\right)^2-4\left(m-4\right)\left(m-5\right)\)
\(=4m^2-32m+64-4\left(m^2-9m+20\right)\)
\(=4m^2-32m+64-4m^2+36m-80\)
=4m-16
Để bất phương trình luôn âm thì \(\left\{{}\begin{matrix}4m-16< 0\\m-4< 0\end{matrix}\right.\Leftrightarrow m< 4\)
Vậy: m<=4
Câu 1 a.tìm tất cả các giá trị của tham số m để bất phương trình mx²+3mx+(m+1)>0 nghiệm đúng với mọi số thực x?
b.tìm các giá trị của m để biểu thức sau luôn âm:g(x)=(m-4)x²+(2m-8)x+m-5
Cho phương trình \(x^2-\left(m+1\right)x+2-8=0\) (1), m là tham số.
a) giải phương trình (1) khi m=2.
b) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn
\(x^2_1+x_2^2+\left(x1-2\right)\left(x2-2\right)=11\)
a:Sửa đề: x^2-(m+1)x+2m-8=0
Khi m=2 thì (1) sẽ là x^2-3x-4=0
=>(x-4)(x+1)=0
=>x=4 hoặc x=-1
b: Δ=(-m-1)^2-4(2m-8)
=m^2+2m+1-8m+32
=m^2-6m+33
=(m-3)^2+24>=24>0
=>(1) luôn có hai nghiệm pb
\(x_1^2+x_2^2+\left(x_1-2\right)\left(x_2-2\right)=11\)
=>(x1+x2)^2-2x1x2+x1x2-2(x1+x2)+4=11
=>(m+1)^2-(2m-8)-2(m+1)+4=11
=>m^2+2m+1-2m+8-2m-2+4=11
=>m^2-2m=0
=>m=0 hoặc m=2
Tìm các giá trị của m để phương trình x 2 – 2(m + 1)x + 2m = 0 có hai nghiệm x 1 ; x 2 thỏa mãn x 1 3 + x 2 3 = 8
A. m = 1
B. m = −1
C. m = 0
D. m > −1
Phương trình x2 – 2(m + 1)x + 2m = 0 có a = 1 ≠ 0 và
∆ ' = ( m + 1 ) 2 – 2 m = m 2 + 1 > 0 ; m nên phương trình luôn có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = 2 m + 1 x 1 . x 2 = 2 m
Xét x 1 3 + x 2 3 = 8 ( x 1 + x 2 ) 3 − 3 x 1 . x 2 ( x 1 + x 2 ) = 8
⇔ [ 2 ( m + 1 ) ] 3 – 3 . 2 m . [ 2 ( m + 1 ) ] = 8
8 ( m 3 + 3 m 2 + 3 m + 1 ) – 6 m ( 2 m + 2 ) = 8 ⇔ 8 m 3 + 12 m 2 + 12 m = 0
⇔ m ( 2 m 2 + 3 m + 3 ) = 0
⇔ m = 0 2 m 2 + 3 m + 3 = 0
Phương trình 2 m 2 + 3 m + 3 = 0 c ó ∆ 1 = 3 2 – 4 . 2 . 3 = − 15 < 0 nên phương trình này vô nghiệm
Vậy m = 0 là giá trị cần tìm
Đáp án: C
Cho phương trình x2 - (m + 2)x + m + 8 = 0 (1) với m là tham số
a.Giải phương trình (1) khi m = -8
b.Tìm các giá trị của m để phương trình (1) có hai nghiệm dương phân biệt x1,x2 thỏa mãn x13 - x2 = 0
a: Khi m=-8 thì (1) sẽ là x^2+6x=0
=>x=0; x=-6
Cho hàm số f x = x − 3 3 x 2 + 8. Tính tổng các giá trị nguyên của m để phương trình f x − 1 + m = 2 có đúng 3 nghiệm phân biệt.
A. -2
B. -6
C. 8
D. 4
Chọn B.
Phương pháp:

Bảng biến thiên:
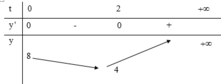
Phương trình đã cho có 3 nghiệm ⇔ phương trình ẩn t có hai nghiệm phân biệt trong đó có một nghiệm bằng 0 và một nghiệm dương ⇔ đường thẳng y = 2-m cắt đồ thị hàm số tại một điểm có hoành độ bằng 0 và điểm còn lại có hoành độ dương.
