Biết rằng 9 x + 9 − x = 23. Khi đó biểu thức A = 5 + 3 x + 3 − x 1 − 3 x − 3 − x = a b với a b là phân số tối giản và a , b ∈ ℤ . Tích a.b có giá trị bằng
A. 10
B. 8
C. -8
D. -10
Biết rằng 9x + 9–x = 23. Khi đó biểu thức A = 5 + 3 x + 3 - x 1 - 3 x - 3 - x = a b với a b là phân số tối giản và a , b ∈ ℤ . Tích a.b có giá trị bằng
A. 10.
B. 8.
C. -8.
D. -10.
Đáp án D.
Ta có 9x + 9–x = 23
⇔ 3 x 2 + 1 3 x 2 = 23 ⇔ 3 x 2 + 2 . 3 x . 1 3 x + 1 3 x 2 = 25
=> 3x + 3–x = 5.
V ậ y A = 5 + 5 1 - 5 = - 5 2 = a b
→ a . b = - 5 . 2 = - 10 .
Cho 9 x + 9 − x = 23. Khi đó biểu thức A = 5 + 3 x + 3 − x 1 − 3 x − 3 − x = a b với a b tối giản và a , b ∈ ℤ . Tích a . b có giá trị bằng:
A. 8
B. 10
C. -8
D. -10
Đáp án D
Phương pháp: Biến đổi phương trình đã cho để tính 3 x + 3 − x , từ đó thay vào biểu thức A
Cách giải:
Ta có: 9 x + 9 − x = 23
⇔ 3 x + 3 − x 2 = 25 ⇔ 3 x + 3 − x = 5 vì 3 x + 3 − x > 0 , ∀ x ∈ R
⇒ A = 5 + 3 x + 3 − x 1 − 3 x − 3 − x = 5 + 5 1 − 5 = − 5 2 = a b
Vậy a b = − 10
Chú ý khi giải:
HS thường phân vân ở chỗ tính 3 x + 3 − x vì đến đó các em không biết nhận xét 3 x + 3 − x > 0 , ∀ x dẫn đến một số em có thể chọn nhầm đáp án.
Tính rồi so sánh giá trị của hai biểu thức (theo mẫu).
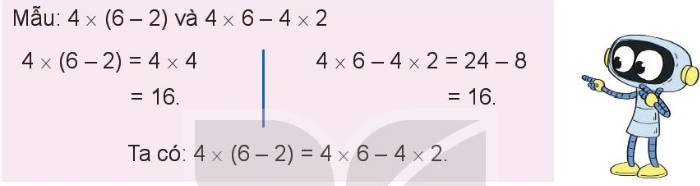
a) 23 x (7 - 4) và 23 x 7 - 23 x 4
b) (8 - 3) x 9 và 8 x 9 - 3 x 9
a,
23 x (7 - 4) = 23 x 3 = 69
23 x 7 - 23 x 4 = 161 - 92 = 69
Ta có: 23 x (7 - 4) = 23 x 7 - 23 x 4
b,
(8 - 3) x 9 = 5 x 9 = 45
8 x 9 - 3 x 9 = 72 - 27 = 45
Ta có: (8 - 3) x 9 = 8 x 9 - 3 x 9
Câu 18. Tổng các số nguyên x thỏa mãn − 10 13 x là A. 33. B. 47 . C. 23. D. 46
Câu 19. Khi bỏ dấu ngoặc trong biểu thức: 2009 (5 9 2008) − − + ta được A. 2009 5 9 2008 +−− . B. 2009 5 9 2008 − − + . C. 2009 5 9 2008 − + − . D. 2009 5 9 2008 − + + .
Câu 20. Tính nhanh 171 [( 53) 96 ( 171)] + − + + − . A. −149. B. 43. C. 149. D. −43.
Câu 21. Giá trị của biểu thức − − + − − 15 17 12 (12 15) bằng A. −12 . B. −15. C. −17. D. −18. Câu 22. Tìm x biết ( 5) ( 2) 2 ( 15) − − = − − x A. −3. B. −2 . C. −5. D. −4 .
Bài 1. (2,0 điểm) Cho biểu thức:
và
với
a) Tính giá trị biểu thức B khi x = 9.
b) Rút gọn A
c) Chứng minh rằng khi A > 0 thì
a) \(B=\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{9-\sqrt{9}+1}{\sqrt{9}-1}=\dfrac{9-3+1}{3-1}=\dfrac{7}{2}\)
b) \(A=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+2\left(\sqrt{x}-2\right)-9\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
c) \(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}>0\Leftrightarrow\sqrt{x}-1>0\left(do.\sqrt{x}+3>0\right)\)
\(\Leftrightarrow\sqrt{x}>1\Leftrightarrow x>1\)
\(B=\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+1}{\sqrt{x}-1}=\sqrt{x}+\dfrac{1}{\sqrt{x}-1}\)
Do \(\sqrt{x}>1\Leftrightarrow\sqrt{x}-1>0\)
Áp dụng BĐT Cauchy cho 2 số k âm:
\(B=\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}+1\ge2\sqrt{\left(\sqrt{x}-1\right).\dfrac{1}{\sqrt{x}-1}}+1=2+1=3\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=1\Leftrightarrow x=4\)
Tính gia trị của biểu thức:
a). 23 x 57 + 42 x 23 + 23.
b). 2/9 x 5/7 + 2/9 x 2/7
Giup tớ ,tớ tk cho, làm chi tiết giùm mình luôn nhé!
a) \(23\times57+42\times23+23=23\times\left(57+42+1\right)\)
\(=23\times100=2300\)
b) \(\frac{2}{9}\times\frac{5}{7}+\frac{2}{9}\times\frac{2}{7}=\frac{2}{9}\times\left(\frac{5}{7}+\frac{2}{7}\right)\)
\(=\frac{2}{9}\times1=\frac{2}{9}\)
a) 23 x 57 + 42 x 23 + 23
= 23 x ( 57 + 42 + 1 )
= 23 x 100
= 2300
b) \(\frac{2}{9}\times\frac{5}{7}+\frac{2}{9}\times\frac{2}{7}\)
\(=\frac{2}{9}\times\left(\frac{5}{7}+\frac{2}{7}\right)\)
\(=\frac{2}{9}\times1\)
\(=\frac{2}{9}\)
Học tốt #
a) \(23\text{}\times57+42\text{}\times23+23\)
\(=23\text{}\times\left(57+42+1\right)\)
\(=23\text{}\times100\)
\(=2300\)
b) \(\frac{2}{9}\text{}\times\frac{5}{7}+\frac{2}{9\text{}}\text{}\times\frac{2}{7}\)
\(=\frac{2}{9}\text{}\times\left(\frac{5}{7}+\frac{2}{7}\right)\)
\(=\frac{2}{9}\text{}\times1\)
\(=\frac{2}{9}\)
_Chúc bạn học tốt_
Với x ≥ 0, x ≠ 9, cho các biểu thức:
P = 2 x x + 3 + x x - 3 - 3 x + 3 x - 9 và Q = x + 1 x - 3
a, Tính giá trị của Q tại x = 7 - 4 3
b, Rút gọn P
c, Tìm x để M ≥ - 2 3 biết M = P Q
d, Đặt A = x . M + 4 x + 7 x + 3 . Tìm giá trị nhỏ nhất của A
a, Từ x = 7 - 4 3 tìm được x = 2 - 3 . Thay vào Q và tính ta được Q = 3 - 3 1 + 3
b, P = 3 x + 3 9 - x
c, Tìm được
M
=
P
Q
=
-
3
x
+
3
Giải M ≥ - 2 3 ta tìm được 9 4 ≤ x ≠ 9
d, Tìm được A = x + 7 x + 3
Ta có A = x + 1 + 6 x + 3 ≥ 2 x + 6 x + 3 = 2
Từ đó đi đến kết luận A m i n = 2 => x = 1
* Cách khác: A = x + 7 x + 3 = x - 3 + 16 x + 3
= x + 3 + 16 x + 3 - 6 ≥ 2 16 - 6 = 2
=> Kết luận
Tìm GTLN của biểu thức : A = 9 - 4 ( x - 3)^2 B= - | 23 - x | + 12
Ta có : 4(x - 3) 2 >= 0
=> 9 - 4(x - 3) 2 \(\le\) 9
Max A là 9
Dấu "=" xảy ra<=> x - 3 = 0 <=> x = 3
Vậy...