Gọi x 0 là nghiệm dương nhỏ nhất của phương trình 3 . sin 2 x + 2 . sin x . cos x - cos 2 x = 0 . Chọn khẳng định đúng?
![]()
![]()
![]()
![]()
1) nghiệm dương nhỏ nhất của phương trình \(cot\left(x-\dfrac{\pi}{6}\right)=\sqrt{3}\) là
2) phương trình \(sin\left(\dfrac{2x}{3}+\dfrac{\pi}{3}\right)=0\) có nghiệm là
3) họ nghiệm của phương trình \(cot\)(2x - 30 độ) = \(\sqrt{3}\) là
Nghiệm dương nhỏ nhất của phương trình \(sin\left( {x + \frac{\pi }{6}} \right) - sin2x = 0\;\) là bao nhiêu?
Xét phương trình \(sin\left( {x + \frac{\pi }{6}} \right) - sin2x = 0\;\)
\(\begin{array}{l} \Leftrightarrow sin\left( {x + \frac{\pi }{6}} \right) = sin2x.\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{6} = 2x + k2\pi \\x + \frac{\pi }{6} = \pi - 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Với \(x = \frac{\pi }{6} + k2\pi \) có nghiệm dương bé nhất là \(x = \frac{\pi }{6}\) khi \(k = 0\).
Với \(x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\) có nghiệm dương bé nhất là \(x = \frac{{5\pi }}{{18}}\) khi \(k = 0\).
Vậy nghiệm dương bé nhất của phương trình đã cho là \(x = \frac{\pi }{6}\).
Nghiệm dương bé nhất của phương trình 2 . sin 2 x + 5 . sin x - 3 = 0 là
![]()
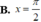
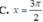
![]()
Tìm nghiệm dương nhỏ nhất của phương trình
\(\cos\pi\left(x^2+2x-\dfrac{1}{2}\right)=\sin\left(\pi x^2\right)\)
\(\Leftrightarrow cos\left(\pi x^2+2\pi x-\dfrac{\pi}{2}\right)=sin\left(\pi x^2\right)\)
\(\Leftrightarrow sin\left(\pi x^2+2\pi x\right)=sin\left(\pi x^2\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\pi x^2+2\pi x=\pi x^2+k2\pi\\\pi x^2+2\pi x=\pi-\pi x^2+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\left(1\right)\\2x^2+2x-2k-1=0\left(2\right)\end{matrix}\right.\)
(1) có nghiệm dương nhỏ nhất \(x=1\)
Xét (2), để (2) có nghiệm \(\Rightarrow\Delta'=1+2\left(2k+1\right)\ge0\) \(\Rightarrow k\ge0\)
Khi đó (2) có 2 nghiệm: \(\left[{}\begin{matrix}x=\dfrac{-1-\sqrt{4k+3}}{2}< 0\\x=\dfrac{-1+\sqrt{4k+3}}{2}\ge\dfrac{\sqrt{3}-1}{2}\end{matrix}\right.\)
\(\Rightarrow\) Nghiệm dương nhỏ nhất của pt đã cho là \(x=\dfrac{\sqrt{3}-1}{2}\)
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Nghiệm dương nhỏ nhất của phương trình sinx+sin 2x=cos x+\(2cos^2x\) là
Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình −4x + 3y = 8. Tính x + y
A. 5
B. 6
C. 7
D.
Ta có −4x + 3y = 8 ⇔ y = 4 x + 8 3 ⇔ y = x + x + 8 3
Đặt x + 8 3 = t ⇒ x = 3t – 8 ⇒ y = 3t – 8 + t ⇒ y = 4t – 8 ( )
Nên nghiệm nguyên của phương trình là x = 3 t − 8 y = 4 t − 8 t ∈ ℤ
Vì x, y nguyên dương nên x > 0 y > 0 ⇒ 3 t − 8 > 0 4 t − 8 > 0 ⇒ t > 8 3 t > 2 ⇒ t > 8 3
mà t ∈ ℤ ⇒ t ≥ 3
Nghiệm nguyên dương nhỏ nhất của phương trình là x = 3.3 − 8 y = 4.3 − 8 ⇔ x = 1 y = 4
⇒ x + y = 5
Đáp án: A
Gọi (x; y) là nghiệm nguyên dương nhỏ nhất của phương trình 6x − 7y = 5. Tính x – y
A. 2
B. 3
C. 1
D. −1
Ta có 6x – 7y = 5 ⇔ x = 7 y + 5 6 ⇔ x = y + y + 5 6
Đặt y + 5 6 = t t ∈ ℤ ⇒ y = 6t – 5 = 6 ⇒ x = y + y + 5 6 = 6t – 5 + t = 7t – 5
Nên nghiệm nguyên của phương trình là x = 7 t − 5 y = 6 t − 5 t ∈ ℤ
Vì x, y nguyên dương nên x > 0 y > 0 ⇒ 7 t − 5 > 0 6 t − 5 > 0 ⇒ t > 5 7 t > 5 6 ⇒ t > 5 7
mà t ∈ ℤ ⇒ t ≥ 1
Do đó nghiệm nguyên dương nhỏ nhất của phương trình có được khi t = 1
⇒ x = 7.1 − 5 y = 6.1 − 5 ⇒ x = 2 y = 1 ⇒ x − y = 1
Đáp án: C
Gọi x 0 là nghiệm dương nhỏ nhất của phương trình 3 sin 2 x + 2 sin x cos x - cos 2 x = 0 . Chọn khẳng định đúng?
A. x 0 ∈ π 2 ; π
B. x 0 ∈ 3 π 2 ; 2 π
C. x 0 ∈ 0 ; π 2
D. x 0 ∈ π ; 3 π 2
Phương trình:
3 sin 2 x + 2 sin x cos x - cos 2 x = 0 (*).
cos x = 0 ⇒ sin 2 x = 1 không phải là nghiệm của phương trình (*).
cos x ≠ 0 . Ta có:
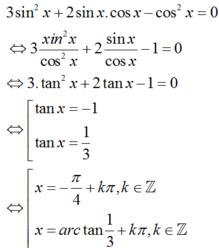
Nghiệm nguyên dương nhỏ nhất của phương trình là x 0 ∈ 0 ; π 2
Chọn C.