Tìm giao điểm của hai đường thẳng:
( d 1 ): ax + 2y = -3 và ( d 2 ): 3x – by = 5, biết rằng ( d 1 ) đi qua điểm M(3; 9) và ( d 2 ) đi qua điểm N(-1; 2).
Tìm a và b biết đường thẳng y = ax + b đi qua hai điểm A(2;-1) và B (1;-3) b tìm toạ độ giao điểm của hai đường thẳng (d1) 2x+y=-3 và (d2) 3x-2y=-1
a: Theo đề, ta có hệ:
2a+b=-1 và a+b=-3
=>a=2 và b=-5
b; tọa độ giao là:
2x+y=-3 và 3x-2y=-1
=>x=-1 và y=-1
Cho hàm số y = 2x + 3 (d) và y = x − 1 (d’)
a, Tìm tọa độ giao điểm M của hai đường thẳng (d) và (d’).
b, Tìm hệ số a và b của hàm số y = ax + b có đồ thị đi qua điểm (−2; 3) và song song với đường thẳng (d).
a. \(PTHDGD:\left(d\right)-\left(d'\right):2x+3=x-1\)
\(\Rightarrow x=-4\left(1\right)\)
Thay (1) vào (d'): \(y=-4-1=-5\)
\(\Rightarrow M\left(-4;-5\right)\)
\(a,\text{PT hoành độ giao điểm: }2x+3=x-1\\ \Leftrightarrow x=-4\Leftrightarrow y=-5\\ \Leftrightarrow M\left(-4;-5\right)\\ b,\Leftrightarrow\left\{{}\begin{matrix}-2a+b=3\\a=2;b\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=7\end{matrix}\right.\)
Bài 3. Trên mặt phẳng Oxy, cho đường thẳng (d): y = ax+b với a, b là hằng số. Tìm a, b biết:
a) d đi qua điểm M(1;−2) và song song với đường thẳng d_{1}:y=2x-1
b) d đi qua gốc tọa độ và qua giao điểm của hai đường thẳng d_{2}:y=4x-3 và d_{3}:y=-x+3.
c) d cắt trục hoành tại điểm có hoành độ bằng 5 và đi qua điểm M(2;3).
d) d cắt đường thẳng dạ : y=x+1 tại điểm có tung độ bằng 2 và vuông góc với đường thẳng d_{2}:y=3-x.
Cho hàm số: y=ax+b
Tìm a, b biết đồ thị hàm số đã cho song song với đường thẳng (d1): y= 3x - 5 và đi qua giao điểm Q của hai đường thẳng (d2) y= 2x - 3 (d3) y= - 3x + 2
Bằng cách tìm giao điểm của hai đường thẳng d: 4x + 2y = −5 và d’: 2x – y = −1 ta tìm được nghiệm của hệ phương trình 4 x + 2 y = − 5 2 x − y = − 1 là ( x 0 ; y 0 ) . Tính x 0 . y 0
A. 21 32
B. − 21 32
C. 21 8
D. − 10 12
Ta có d: 4x + 2y = −5 ⇔ y = − 4 x − 5 2 và d’: 2x – y = −1 ⇔ y = 2x + 1
Xét phương trình hoành độ giao điểm của d và d’:
− 4 x − 5 2 = 2 x + 1 ⇔ −4x – 5 = 4x + 2 ⇔ 8x = −7 ⇔ x = − 7 8
⇒ y = 2 x + 1 = 2. − 7 8 + 1 = − 3 4
Vậy tọa độ giao điểm của d và d’ là − 7 8 ; − 3 4
Suy ra nghiệm của hệ phương trình 4 x + 2 y = − 5 2 x − y = − 1 là x 0 ; y 0 = − 7 8 ; − 3 4
Từ đó x 0. y 0 = − 7 8 . − 3 4 = 21 32
Đáp án: A
giúp mình giải bài sau với:
Cho hai đường thẳng y = 2x + 2 (d₁) và y = 6 - 2x (d2)
a/ Vẽ (d₁) và (d2) trên cùng một mặt phẳng tọa độ.
b/ Tìm tọa độ giao điểm của (d₁) và (d2) bằng phép tính.
c/ Tìm a,b của đường thẳng (d) y=ax+b biết đường thẳng (d) cắt đường thẳng y = x - 6 tại một điểm trên trục tung và cắt đường cắt đường thẳng y = 2x+1 tại điểm có hoành độ bằng 2.
a: 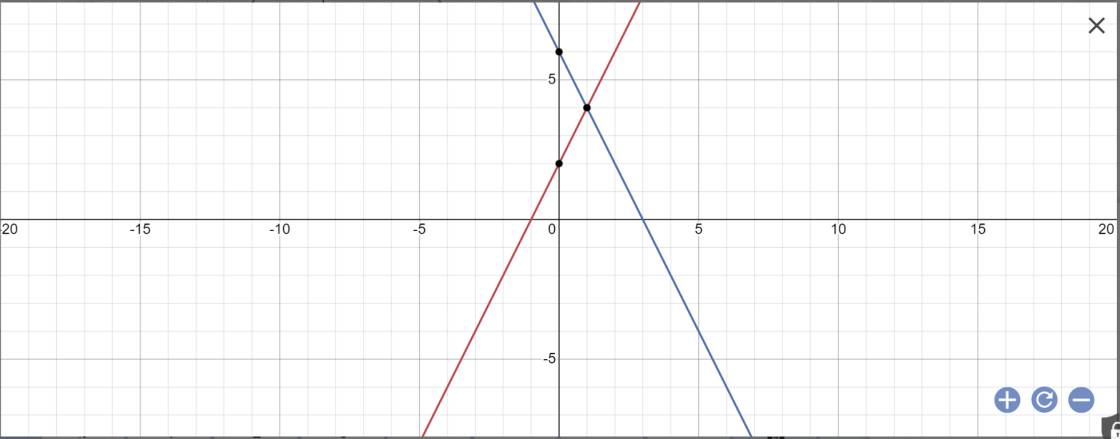
b: Phương trình hoành độ giao điểm là:
2x+2=6-2x
=>2x+2x=6-2
=>4x=4
=>x=1
Thay x=1 vào y=2x+2, ta được:
\(y=2\cdot1+2=4\)
Vậy: (d1) cắt (d2) tại A(1;4)
c: Thay x=0 vào y=x-6, ta được:
y=0-6=-6
Thay x=0 và y=-6 vào y=ax+b, ta được:
\(a\cdot0+b=-6\)
=>b=-6
=>y=ax-6
Thay x=2 vào y=2x+1, ta được:
\(y=2\cdot2+1=5\)
Thay x=2 và y=5 vào y=ax-6, ta được:
2a-6=5
=>2a=11
=>\(a=\dfrac{11}{2}\)
đường thẳng (d) : y = ax +b đi qua hai điểm A (-1;-2 ) và B ( 3;-1
Từ pt đường thẳng d tìm được, hãy tìm phương trình đường thẳng d’ song song với d ?
Lời giải:
Vì $A, B\in (d)$ nên:
\(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -2=-a+b\\ -1=3a+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=\frac{1}{4}\\ b=\frac{-7}{4}\end{matrix}\right.\)
Vậy PTĐT $(d)$ là: $y=\frac{1}{4}x-\frac{7}{4}$
PTĐT $(d')$ song song với $(d)$ có dạng: $y=\frac{1}{4}x+m$ với $m\neq \frac{-7}{4}$
Mong đc bn nào dễ thưng dẽ hình ạ! ٩(๑❛ᴗ❛๑)۶
Cho đường thẳng: (d): y = x + 3 (d’): y = ax + 1
a)Tìm a biết (d’) đi qua điểm M(1;-2).
b) Vẽ (d) và (d’) trên cùng một mặt phẳng tọa độ với a vừa tìm.
c) Tìm tọa độ giao điểm N của đường thẳng (d) và (d’).
d) Tính góc tạo bởi (d) với trục Ox.
cho hàm só y=ax-2 (a≠0), có đồ thị đường thẳng (d)
a) xác định a, biết (d) song song với đường thẳng y=1-3x. vẽ đường thẳng (d)
b) tìm tọa độ giao điểm của đường thẳng (d) và đường thẳng (d'): y=x+6
a.
- Đường thẳng (d) song song với y = 1 - 3x nên ta có:
\(a=-3\)
\(\rightarrow\) Hàm số có dạng \(y=-3x-2\)
- Vẽ đường thẳng \(\left(d\right):y=-3x-2\)
+ Giao với trục Oy: \(x=0\rightarrow y=-2\Rightarrow A\left(0;-2\right)\)
+ Giao với trục Ox: \(y=0\rightarrow x=-\dfrac{2}{3}\Rightarrow B\left(-\dfrac{2}{3};0\right)\)
Nối 2 điểm A và B ta được đường thẳng (d)
b.
- Gọi tọa độ giao điểm của đường thẳng \(\left(d\right)\) và \(\left(d'\right):y=x+6\) là: \(\left(x_0;y_0\right)\)
- Vì \(\left(x_0;y_0\right)\) thuộc đường thẳng \(\left(d\right)\) nên ta có:
\(y_0=-3x_0-2\) (1)
- Vì \(\left(x_0;y_0\right)\) thuộc đường thẳng \(\left(d'\right):y=x+6\) nên ta có:
\(y_0=x_0+6\) (2)
- Từ (1) và (2), ta có:
\(-3x_0-2=x_0+6\)
\(\Leftrightarrow-3x_0-x_0=6+2\)
\(\Leftrightarrow-4x_0=8\)
\(\Leftrightarrow x_0=-2\)
\(\rightarrow y_0=-2+6=4\)
Vậy tọa độ giao điểm 2 đường thẳng đó là: \(\left(-2;4\right)\)