Giải phương trình trùng phương:
a ) 9 x 4 − 10 x 2 + 1 = 0 b ) 5 x 4 + 2 x 2 − 16 = 10 − x 2 c ) 0 , 3 x 4 + 1 , 8 x 2 + 1 , 5 = 0 ; d ) 2 x 2 + 1 = 1 x 2 − 4
a) \(2\left(x^2-2x\right)+\sqrt{x^2-2x-3}-9=0\)
b) \(3\sqrt{2+x}-6\sqrt{2-x}+4\sqrt{4-x^2}=10-3x\)
c) Cho phương trình: \(\sqrt{x}+\sqrt{9-x}=\sqrt{-x^2+9x+m}\)
+) Giải phương trình khi m=9
+) Tìm m để phương trình có nghiệm
a, ĐK: \(x\le-1,x\ge3\)
\(pt\Leftrightarrow2\left(x^2-2x-3\right)+\sqrt{x^2-2x-3}-3=0\)
\(\Leftrightarrow\left(2\sqrt{x^2-2x-3}+3\right).\left(\sqrt{x^2-2x-3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2-2x-3}=-\dfrac{3}{2}\left(l\right)\\\sqrt{x^2-2x-3}=1\end{matrix}\right.\)
\(\Leftrightarrow x^2-2x-3=1\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow x=1\pm\sqrt{5}\left(tm\right)\)
b, ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{2+x}-2\sqrt{2-x}=t\Rightarrow t^2=10-3x-4\sqrt{4-x^2}\)
Khi đó phương trình tương đương:
\(3t-t^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}-2\sqrt{2-x}=0\\\sqrt{2+x}-2\sqrt{2-x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2+x=8-4x\\2+x=17-4x+12\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(tm\right)\\5x-15=12\sqrt{2-x}\left(1\right)\end{matrix}\right.\)
Vì \(-2\le x\le2\Rightarrow5x-15< 0\Rightarrow\left(1\right)\) vô nghiệm
Vậy phương trình đã cho có nghiệm \(x=\dfrac{6}{5}\)
c, ĐK: \(0\le x\le9\)
Đặt \(\sqrt{9x-x^2}=t\left(0\le t\le\dfrac{9}{2}\right)\)
\(pt\Leftrightarrow9+2\sqrt{9x-x^2}=-x^2+9x+m\)
\(\Leftrightarrow-\left(-x^2+9x\right)+2\sqrt{9x-x^2}+9=m\)
\(\Leftrightarrow-t^2+2t+9=m\)
Khi \(m=9,pt\Leftrightarrow-t^2+2t=0\Leftrightarrow\left[{}\begin{matrix}t=0\\t=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}9x-x^2=0\\9x-x^2=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=9\left(tm\right)\\x=\dfrac{9\pm\sqrt{65}}{2}\left(tm\right)\end{matrix}\right.\)
Phương trình đã cho có nghiệm khi phương trình \(m=f\left(t\right)=-t^2+2t+9\) có nghiệm
\(\Leftrightarrow minf\left(t\right)\le m\le maxf\left(t\right)\)
\(\Leftrightarrow-\dfrac{9}{4}\le m\le10\)
giúp vs ạ
1.xác định hệ số a,b,c của phương trình bâc hai 4x2+ 5x-2019=0
2. tính chu vi hình tròn có bán kính bằng 5cm
3.cho hàm số y=(5m+10)x2 tìm m để hàm số đồng biến khi x>0
4.Vẽ đồ thị hàm số (P):y=X2
5 Giải phương trình trùng phương x4- 8x2-9 =0
6 tính tổng và tính tích các nghiệm của PT 2x3-3x-2=0
5:
=>x^4-9x^2+x^2-9=0
=>x^2-9=0
=>x=3; x=-3
4: 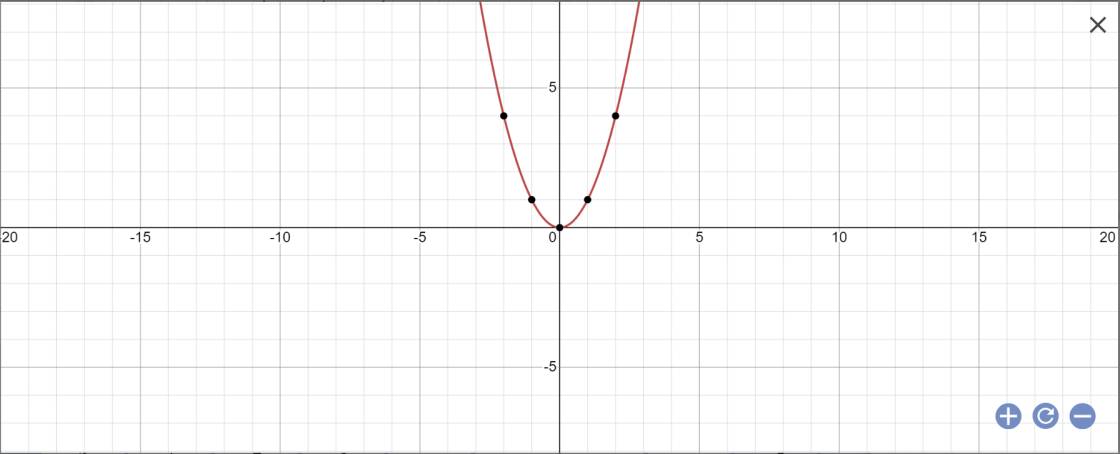
3: HS đồng biến khi x>0
=>5m+10>0
=>m>-2
Giải phương trình trùng phương: 5 x 4 + 2 x 2 - 16 = 10 - x 2
5x4 + 2x2 – 16 = 10 – x2
⇔ 5x4 + 2x2 – 16 – 10 + x2 = 0
⇔ 5x4 + 3x2 – 26 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 5t2 + 3t – 26 = 0 (2)
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 32 – 4.5.(-26) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
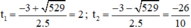
Đối chiếu điều kiện chỉ có t1 = 2 thỏa mãn
+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
Giải các phương trình trùng phương x 4 -8 x 2 – 9 =0
Đặt m = x 2 .Điều kiện m ≥ 0
Ta có: x 4 -8 x 2 – 9 =0 ⇔ m 2 -8m -9 =0
Phương trình m 2 - 8m - 9 = 0 có hệ số a = 1,b = -8,c = -9 nên có dạng a – b + c = 0
suy ra: m 1 = -1 (loại) , m 2 = -(-9)/1 =9
Ta có: x 2 =9 ⇒ x= ± 3
Vậy phương trình đã cho có 2 nghiệm : x 1 =3 ; x 2 =-3

[Ôn thi vào 10]
Bài 1:
a. Tính \(A=\sqrt{8}+\sqrt{18}-\sqrt{32}\)
b. Rút gọn biểu thức \(B=\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
Bài 2:
a. Giải hệ phương trình: \(\left\{{}\begin{matrix}2x-3y=4\\x+3y=2\end{matrix}\right.\)
b. Giải phương trình: \(\dfrac{10}{x^2-4}+\dfrac{1}{2-x}=1\)
Bài 3:
Một đội thợ mỏ phải khai thác 260 tấn than trong một thời hạn nhất định. Trên thực tế, mỗi ngày đội đều khai thác vượt định mức 3 tấn, do đó họ đã khai thác được 261 tấn than và xong trước thời hạn một ngày.
Hỏi theo kế hoạch mỗi ngày đội thợ phải khai thác bao nhiêu tấn than?
Bài 1:
a) \(A=\sqrt{8}+\sqrt{18}-\sqrt{32}\)
\(=2\sqrt{2}+3\sqrt{2}-4\sqrt{2}\)
\(=\sqrt{2}\)
b) \(B=\sqrt{9-4\sqrt{5}}-\sqrt{5}\)
\(=\sqrt{4-4\sqrt{5}+5}-\sqrt{5}\)
\(=\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{5}\)
\(=\left|2-\sqrt{5}\right|-\sqrt{5}\)
\(=\sqrt{5}-2-\sqrt{5}\)
\(=-2\)
Bài 2:
a) \(\left\{{}\begin{matrix}2x-3y=4\\x+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x=6\\x+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\2+3y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
b) ĐKXĐ: \(x\ne\pm2\)
Với \(x\ne\pm2\), ta có:
\(\dfrac{10}{x^2-4}+\dfrac{1}{2-x}=1\)
\(\Leftrightarrow\dfrac{10}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}=1\)
\(\Leftrightarrow\dfrac{10-x-2}{x^2-4}=1\)
\(\Leftrightarrow\dfrac{8-x}{x^2-4}=1\)
\(\Rightarrow x^2-4=8-x\)
\(\Leftrightarrow x^2+x-12=0\)
\(\Leftrightarrow x^2-3x+4x-12=0\)
\(\Leftrightarrow x\left(x-3\right)+4\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\) (TM)
Vậy phương trình có tập nghiệm là: S ={3; -4}
Gọi số tấn than mỗi ngày đội thợ phải khai thác theo kế hoạch là: x(tấn). 0 < x <260
Số tấn than đã khai thác thực tế trong mỗi ngày là: x + 3 (tấn)
Số ngày mà đội thợ khai thác 260 tấn trong kế hoạch là: \(\dfrac{260}{x}\) (ngày)
Số ngày mà đội thợ khai thác 261 tấn thực tế là: \(\dfrac{261}{x+3}\) (ngày)
Vì trên thực tế, mỗi ngày đội đều khai thác vượt định mức 3 tấn, do đó họ đã khai thác được 261 tấn than và xong trước thời hạn một ngày nên ta có phương trình:
\(\dfrac{261}{x+3}+1=\dfrac{260}{x}\)
\(\Leftrightarrow\dfrac{261+x+3}{x+3}=\dfrac{260}{x}\)
\(\Leftrightarrow\dfrac{264+x}{x+3}=\dfrac{260}{x}\)
\(\Rightarrow260\left(x+3\right)=x\left(264+x\right)\)
\(\Leftrightarrow260x+780=264x+x^2\)
\(\Leftrightarrow x^2+4x-780=0\)
\(\Leftrightarrow x^2-26x+30x-780=0\)
\(\Leftrightarrow x\left(x-26\right)+30\left(x-26\right)=0\)
\(\Leftrightarrow\left(x-26\right)\left(x+30\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-26=0\\x+30=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=26\left(TM\right)\\x=-30\left(loại\right)\end{matrix}\right.\)
Vậy số tấn than mỗi ngày đội thợ phải khai thác theo kế hoạch là: 26 tấn
giải phương trình (x-9)^4+(x-10)^4=(19-2x)^4
Giải phương trình trùng phương: 2 x 2 + 1 = 1 x 2 - 4
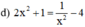
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2x4 + x2 = 1 – 4x2
⇔ 2x4 + x2 + 4x2 – 1 = 0
⇔ 2x4 + 5x2 – 1 = 0 (1)
Đặt t = x2, điều kiện t > 0.
Khi đó (1) trở thành : 2t2 + 5t – 1 = 0 (2)
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 52 – 4.2.(-1) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
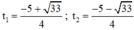
Đối chiếu với điều kiện thấy có nghiệm t1 thỏa mãn.
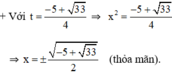
Vậy phương trình có tập nghiệm 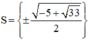
Giải các phương trình trùng phương: x4 – 5x2 + 4 = 0
x4 – 5x2 + 4 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t2 – 5t + 4 = 0 (2)
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
Giải các phương trình trùng phương:
a ) x 4 − 5 x 2 + 4 = 0 b ) 2 x 4 − 3 x 2 − 2 = 0 c ) 3 x 4 + 10 x 2 + 3 = 0
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
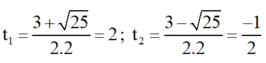
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
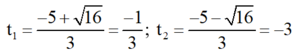
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.