Tập xác định của hàm số f ( x ) = 1 1 - cos x là:
![]()
![]()
![]()
![]()
Cho hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) có \(f(0) = 1,f(1) = 2,f(2) = 5.\)
a) Hãy xác định giá trị của các hệ số \(a,b\) và \(c.\)
b) Xác định tập giá trị và khoảng biến thiên của hàm số.
Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)
Tìm tập xác định D của hàm số f ( x ) = 1 x ; x ≥ 1 x + 1 ; x < 1
A. D = {−1}.
B. D = R
C. D = [-1;+ ∞ )
D. D = [−1; 1)
Tập xác định của hàm số f (x)=\(\sqrt{x-3}\) + \(\dfrac{1}{\sqrt{1-x}}\).
Cho hàm số:
\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
a) Tìm tập xác định của hàm số
b) Tìm x để f(x) nguyên
Sửa b)`->` x nguyên để f(x) nguyên
a)TXĐ:`{(x>=0),(sqrtx-1 ne 0):}`
`<=>{(x>=0),(sqrtx ne 1):}`
`=>x>=0,x ne 1`
`b)f(x) in ZZ=>sqrtx+1 vdots sqrtx-1`
`=>sqrtx-1+2 vdots sqrtx-1`
`=>2 vdots sqrtx-1`
`=>sqrtx-1 in Ư(2)`
`=>sqrtx-1 in {+-1;2}`
`=>sqrtx in {0;2;3}`
`=>x in {0;4;9}`
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b: Để f(x) nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;2;3\right\}\)
hay \(x\in\left\{0;4;9\right\}\)
Tập xác định của hàm số f ( x ) = 2 x - 1 + 1 x 2 - 4 là
![]()
![]()
![]()
![]()
Tập xác định của hàm số f(x) = - x 2 + 2 x x 2 + 1 là tập hợp nào sau đây?
A. ℝ \{-1;1}
B. ℝ
C. ℝ \1}
D. ℝ \{-1}
Chọn B
Phương pháp:
Sử dụng phân thức có nghĩa khi mẫu thức khác 0 để tìm xác định của hàm số.
Cách giải:
Điều kiện: ![]()
![]()
Suy ra tập xác định D = ℝ .
Tập xác định của hàm số f ( x ) = - x 2 + 2 x x 2 + 1 là tập hợp nào sau đây?
A. R \ - 1 ; 1
B.R
C. R \ 1
D. R \ - 1
Tìm tập xác định của hàm số :
\(f\left(x\right)=\dfrac{sinx+1}{sinx-1}\)
ĐKXĐ:
\(sinx\ne1\Leftrightarrow\ne x\ne\dfrac{\pi}{2}+k2\pi\)
Cho hàm số y = f(x) xác định trên D = − 1 ; + ∞ \ 1 . Dưới đây là một phần đồ thị của y = f(x)
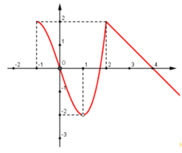
Hỏi trong các mệnh đề sau, có bao nhiêu mệnh đề đúng:
(I) Số điểm cực đại của hàm số trên tập xác định là 1.
(II) Hàm số có cực tiểu là -2 tại x = 1
(III) Hàm số đạt cực đại tại x = 2
(IV) Hàm số đạt cực đại tại x = -1
A. 0
B. 1
C. 2
D. 3

Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B
Tìm tập xác định D của hàm số f ( x ) = 1 2 − x ; x ≥ 1 2 − x ; x < 1
A. D = R
B. D = ( 2 ; + ∞ )
C. D = ( - ∞ ; 2 )
D. D = R\{2}
Đáp án D
Hàm số xác định khi:
x ≥ 1 2 − x ≠ 0 x < 1 2 − x ≥ 0 ⇔ x ≥ 1 x ≠ 2 x < 1 x ≤ 2 ⇔ x ≥ 1 x ≠ 2 x < 1
Vậy xác định của hàm số là D=R\{2}