Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho hàm số y f(x) có bảng biến thiên như sau: (I): Tập xác định của f(x): R {1} (II): Hàm số f(x) có đúng 1 điểm cực trị (III): min f(x) -2 (IV): A(-1; 3) là điểm cực đại của đồ thị hàm số Trong các phát biểu trên, có bao nhiêu phát biểu đúng? A. 2 B. 3 C. 1 D. 0
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như sau:
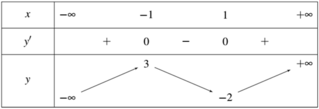
(I): Tập xác định của f(x): R \ {1}
(II): Hàm số f(x) có đúng 1 điểm cực trị
(III): min f(x) = -2
(IV): A(-1; 3) là điểm cực đại của đồ thị hàm số
Trong các phát biểu trên, có bao nhiêu phát biểu đúng?
A. 2
B. 3
C. 1
D. 0
Cho hàm số y f(x) xác định trên tập
D
⊂
R
. Mệnh đề nào sau đây là đúng? A. Điểm cực trị của hàm số là điểm
x
0
∈
D
mà khi đi qua nó, đạo hàm f(x) đổi dấu B. Điểm cực trị của hàm số là điểm
x
0
∈
D
sao cho
f
x
0
0
C. Điểm cực...
Đọc tiếp
Cho hàm số y = f(x) xác định trên tập D ⊂ R . Mệnh đề nào sau đây là đúng?
A. Điểm cực trị của hàm số là điểm x 0 ∈ D mà khi đi qua nó, đạo hàm f'(x) đổi dấu
B. Điểm cực trị của hàm số là điểm x 0 ∈ D sao cho f ' x 0 = 0
C. Điểm cực trị của hàm số là điểm x 0 ∈ D thỏa mãn hàm số đổi chiều biến thiên khi đi qua nó
D. Điểm cực trị của hàm số là điểm x 0 ∈ D sao cho f x 0 là giá trị lớn nhất hoặc nhỏ nhất của hàm số trên tập D .
Cho hàm số yf(x) xác định, liên tục trên tập R{1} và có bảng biến thiên:Khẳng định nào dưới đây là đúng? A. Hàm số đồng biến trên R{1} B. Hàm số đồng biến trên tập
(
-
∞
;
1
)
∪
(
1
;
+
∞
)
C. Hàm số đồng biến trên tập
(
-
∞
;
+
∞
)
D. Hàm số đồng biến trên các khoản...
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên:
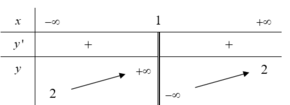
Khẳng định nào dưới đây là đúng?
A. Hàm số đồng biến trên R\{1}
B. Hàm số đồng biến trên tập ( - ∞ ; 1 ) ∪ ( 1 ; + ∞ )
C. Hàm số đồng biến trên tập ( - ∞ ; + ∞ )
D. Hàm số đồng biến trên các khoảng ( - ∞ ; 1 ) và ( 1 ; + ∞ )
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f(x) thỏa mãn
f
(
x
)
(
1
-
x
)
(
x
+
2
)
g
(
x
)
+
2018
với
g
(
x
)
0
,
∀
x
∈
R
. Hàm số
y
f
(...
Đọc tiếp
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thỏa mãn f ' ( x ) = ( 1 - x ) ( x + 2 ) g ( x ) + 2018 với g ( x ) < 0 , ∀ x ∈ R . Hàm số y = f ( 1 - x ) + 2018 x + 2019 nghịch biến trên khoảng nào dưới đây?
A . ( 1 ; + ∞ ) .
B . ( 0 ; 3 ) .
C . ( - ∞ ; 3 ) .
D . ( 4 ; + ∞ ) .
Cho hàm số yf(x) xác định, liên tục trên R{1} và có bảng biến thiên như sauTìm tập hợp tất cả các giá trị của tham thực m để phương trình f(x)m có nghiệm lớn hơn 2 A.
(
-
∞
;
1
)
B. (3;4) C.
(
1
;
+
∞
)
D.
(
4
;
+
∞
)
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R\{1} và có bảng biến thiên như sau
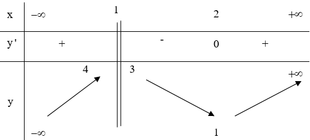
Tìm tập hợp tất cả các giá trị của tham thực m để phương trình f(x)=m có nghiệm lớn hơn 2
A. ( - ∞ ; 1 )
B. (3;4)
C. ( 1 ; + ∞ )
D. ( 4 ; + ∞ )
Cho các mệnh đề sau đây:(1) Ta có biểu thức sau
log
3
x
+
5
+
log
9
x
-
2
2
-
log
3
x
-
1
log
3
x
+...
Đọc tiếp
Cho các mệnh đề sau đây:
(1) Ta có biểu thức sau log 3 x + 5 + log 9 x - 2 2 - log 3 x - 1 = log 3 x + 5 x - 2 x - 1 2
(2) Hàm số log 3 x - 3 2 có tập xác định là D = R.
(3) Hàm số y = log a x có đạo hàm ở tại mọi điểm x > 0 .
(4) Tập xác định D của hàm số y = 2 x - 1 + ln 1 - x 2 là: D = 1 2 ; 1 .
(5) Đạo hàm của hàm số y = 2 x - 1 + ln 1 - x 2 là 1 2 x - 1 - 2 x 1 - x 2 .
Hỏi có bao nhiêu mệnh đề đúng:
A. 2
B. 4
C. 3
D. 5
Cho hàm số
f
(
x
)
ax
3
+
bx
2
+
cx
+
d
có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m(m∈R) sao cho (x-1)
[
m
3
f
(
2
x
-
1
)
-
mf
(
x
)
+
f
(
x
)...
Đọc tiếp
Cho hàm số f ( x ) = ax 3 + bx 2 + cx + d có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của m(m∈R) sao cho (x-1) [ m 3 f ( 2 x - 1 ) - mf ( x ) + f ( x ) - 1 ] ≥0 ∀x∈R. Số phần tử của tập S là
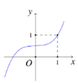
A. 2
B. 0
C. 3
D. 1
Cho hàm số yf(x) xác định, liên tục trên R{1} và có bảng biến thiên như hình dưới đâyTập hợp S tất cả các giá trị của m để phương trình f(x)m có đúng ba nghiệm là A. (-1;1) B. [-1;1] C. {1} D. {-1;1}
Đọc tiếp
Cho hàm số y=f(x) xác định, liên tục trên R\{1} và có bảng biến thiên như hình dưới đây

Tập hợp S tất cả các giá trị của m để phương trình f(x)=m có đúng ba nghiệm là
A. (-1;1)
B. [-1;1]
C. {1}
D. {-1;1}
Cho hàm số y f(x) xác định trên R{-1}, liên tục trên từng khoảng xác định và có bảng biến thiên như dưới đây:Tìm tập hợp tất cả các số thực của m để phương trình f(x)m có nghiệm thực duy nhất
A
.
(
0
;
+
∞
)
∪
-
1
B
.
(
0
;
+
∞
)
C
.
[
0
;...
Đọc tiếp
Cho hàm số y = f(x) xác định trên R\{-1}, liên tục trên từng khoảng xác định và có bảng biến thiên như dưới đây:

Tìm tập hợp tất cả các số thực của m để phương trình f(x)=m có nghiệm thực duy nhất
A . ( 0 ; + ∞ ) ∪ - 1
B . ( 0 ; + ∞ )
C . [ 0 ; + ∞ )
D . [ 0 ; + ∞ ) ∪ - 1