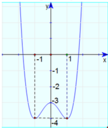
Cho hàm số y = x 4 - 2 x 2 - 3 có đồ thị như hình vẽ bên dưới. Với giá trị nào của tham số m thì phương trình x 4 - 2 x 2 - 3 = 2 m - 4 có hai nghiệm phân biệt?
A. m ≤ 1 2
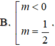
![]()
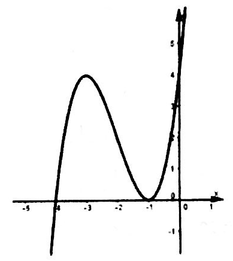
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Cho hàm số y=f(x) có đạo hàm liên tục trên tập R/ 2 và có đồ thị hàm số y=f’(x) như hình vẽ. Biết f 1 ≠ 10 f(3)=4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13
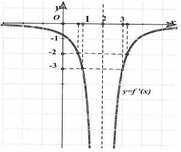
A. 2
B. 1
C. 0.
D. 3
Cho hàm số y = f(x) có đạo hàm f'(x) trên khoảng
(
-
∞
;
+
∞
)
. Đồ thị hàm số y = f(x) như hình vẽ 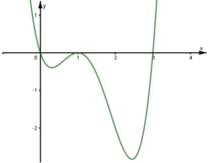
Đồ thị của hàm số y = ( f ( x ) ) 2 có bao nhiêu điểm cực đại, cực tiểu?
A. 2 điểm cực đại, 3 điểm cực tiểu.
B. 1 điểm cực đại, 3 điểm cực tiểu.
C. 2 điểm cực đại, 2 điểm cực tiểu.
A. 3 điểm cực đại, 2 điểm cực tiểu.
Cho hàm sốy=f(x) có đạo hàm f'(x) trên tập số thực ℝ và đồ thị của hàm số y=f(x) như hình vẽ. Khi đó, đồ thị của hàm số y = ( f ( x ) ) 2 có
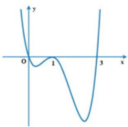
A. 2 điểm cực đại, 2 điểm cực tiểu
B. 2 điểm cực tiểu, 3 điểm cực đại
C. 1 điểm cực đại, 3 điểm cực tiểu
D. 2 điểm cực đại, 3 điểm cực tiểu
Từ đồ thị hàm số f(x) ta thấy đồ thị cắt trục hoành tại ba điểm phân biệt có hoành độ x=0;x=1;x=3
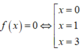
Lại thấy đồ thị hàm số y=f(x) có ba điểm cực trị nên
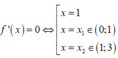
Hàm số y = f x 2 có đạo hàm y'=2f(x).f '(x)
Xét phương trình
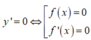
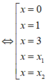
Ta có BXD của y' như sau
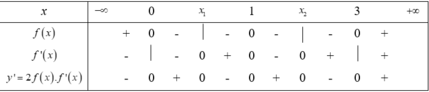
Nhận thấy hàm số y = f x 2 có y' đổi dấu từ âm sang dương tại ba điểm x=0;x=1;x=3 nên hàm số có ba điểm cực tiểu. Và y' đổi dấu từ dương sang âm tại hai điểm x = x 1 ; x = x 2 nên hàm số có hai điểm cực đại.
Chọn đáp án D.
Cho đồ thị hàm số y = f(x) có đạo hàm trên R thỏa mãn f(2) = f(-2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ. Hàm số y = f ( x ) 2 nghịch biến trên khoảng nào trong các khoảng sau?
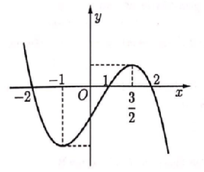
A. - 1 ; 3 2
B. (-2;-1)
C. (-1;1)
D. (1;2)
Cho hàm số y=f(x). Hàm số f'(x) có đồ thị như hĩnh vẽ bên:. Biết f(0) = -4, tìm số điể cực đại của hàm số y= 2.f (f(x)) - [ f(x)]2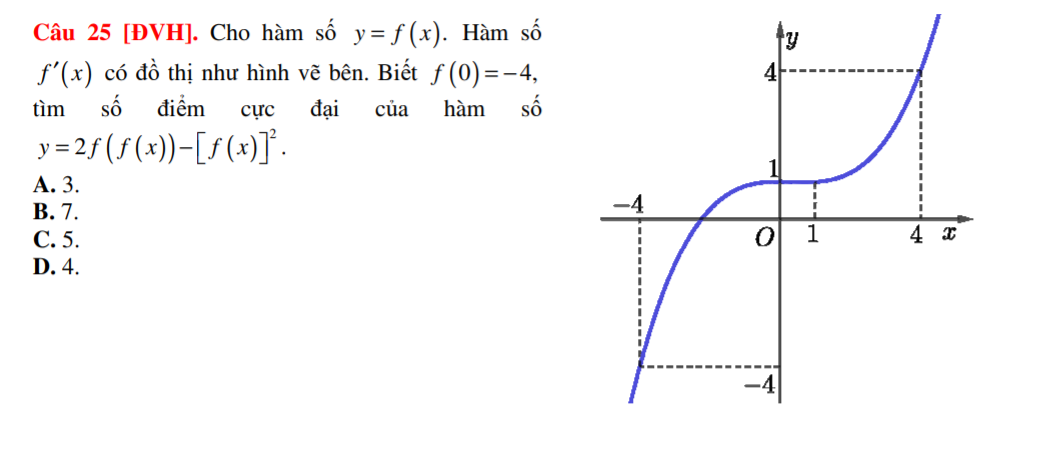
\(y'=2f'\left(x\right).f'\left(f\left(x\right)\right)-2f'\left(x\right).f\left(x\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f'\left(f\left(x\right)\right)=f\left(x\right)\end{matrix}\right.\)
Từ đồ thị ta có \(f'\left(x\right)=0\Rightarrow x=x_1\) với \(-4< x_1< 0\)
Xét phương trình \(f'\left(f\left(x\right)\right)=f\left(x\right)\), đặt \(f\left(x\right)=t\Rightarrow f'\left(t\right)=t\)
Vẽ đường thẳng \(y=t\) (màu đỏ) lên cùng đồ thị \(y=f'\left(t\right)\) như hình vẽ:
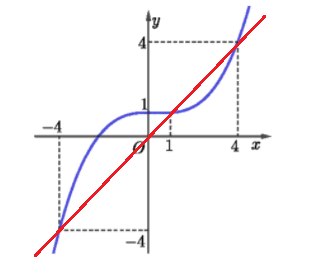
Ta thấy 2 đồ thị cắt nhau tại 3 điểm: \(t=\left\{-4;1;4\right\}\)
\(\Rightarrow\left[{}\begin{matrix}f\left(x\right)=-4\\f\left(x\right)=1\\f\left(x\right)=4\end{matrix}\right.\) (1)
Mặt khác từ đồ thị \(f'\left(x\right)\) và \(f\left(0\right)=-4\) ta được BBT của \(f\left(x\right)\) có dạng:
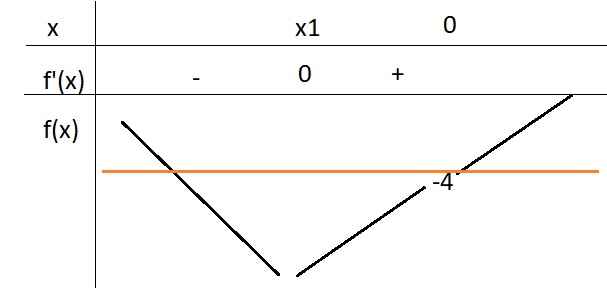
Từ đó ta thấy các đường thẳng \(y=k\ge-4\) luôn cắt \(y=f\left(x\right)\) tại 2 điểm phân biệt
\(\Rightarrow\) Hệ (1) có 6 nghiệm phân biệt (trong đó 3 nghiệm nhỏ hơn \(x_1\) và 3 nghiệm lớn hơn \(x_1\))
Từ đó ta có dấu của y' như sau:

Có 3 lần y' đổi dấu từ dương sang âm nên hàm có 3 cực đại
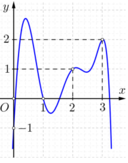
Cho hàm số y = f ( x ) có đồ thị y = f ' ( x ) như hình vẽ bên. Đồ thị hàm số g ( x ) = 2 f ( x ) - ( x - 1 ) 2 có tối đa bao nhiêu điểm cực trị?
A. 3
B. 5
C. 6
D. 7
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho đồ thị của hàm số \(y = {2^x}\) và \(y = 4\) như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình \({2^x} > 4.\)

Khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 là \(\left( {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({2^x} > 4\) là \(\left( {2; + \infty } \right)\)
Cho hàm số y=f(x) có bảng biến thiên như sau
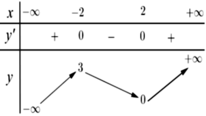
Đồ thị hàm số y= 1 f ( 3 - x ) - 2 có bao nhiêu đường tiệm cận đứng
A. 1
B. 0
C. 2
D. 3
Theo bảng biến thiên ta thấy phương trình ![]() có 3 nghiệm phân biệt. Do đó phương trình
có 3 nghiệm phân biệt. Do đó phương trình ![]() có 3 nghiệm phân biệt.
có 3 nghiệm phân biệt.
Suy ra đồ thị hàm số 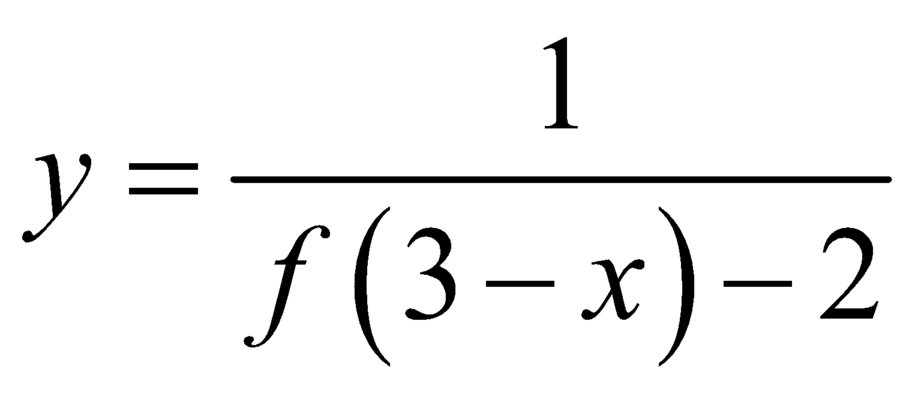 có 3 tiệm cận đứng.
có 3 tiệm cận đứng.
Đáp án D