\(y'=2f'\left(x\right).f'\left(f\left(x\right)\right)-2f'\left(x\right).f\left(x\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}f'\left(x\right)=0\\f'\left(f\left(x\right)\right)=f\left(x\right)\end{matrix}\right.\)
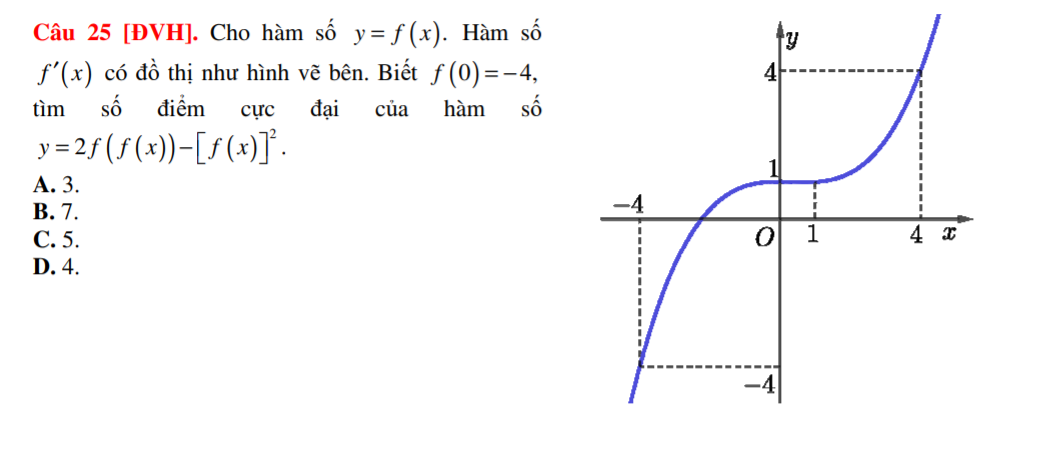
Từ đồ thị ta có \(f'\left(x\right)=0\Rightarrow x=x_1\) với \(-4< x_1< 0\)
Xét phương trình \(f'\left(f\left(x\right)\right)=f\left(x\right)\), đặt \(f\left(x\right)=t\Rightarrow f'\left(t\right)=t\)
Vẽ đường thẳng \(y=t\) (màu đỏ) lên cùng đồ thị \(y=f'\left(t\right)\) như hình vẽ:
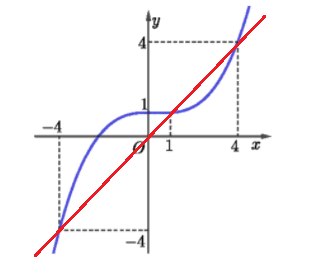
Ta thấy 2 đồ thị cắt nhau tại 3 điểm: \(t=\left\{-4;1;4\right\}\)
\(\Rightarrow\left[{}\begin{matrix}f\left(x\right)=-4\\f\left(x\right)=1\\f\left(x\right)=4\end{matrix}\right.\) (1)
Mặt khác từ đồ thị \(f'\left(x\right)\) và \(f\left(0\right)=-4\) ta được BBT của \(f\left(x\right)\) có dạng:
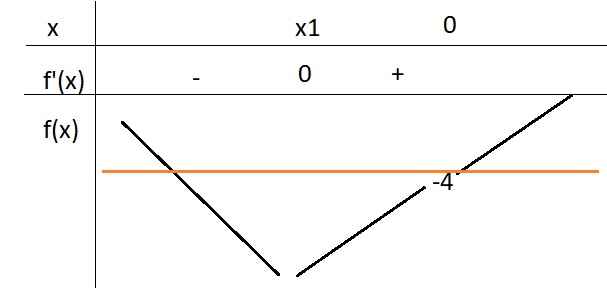
Từ đó ta thấy các đường thẳng \(y=k\ge-4\) luôn cắt \(y=f\left(x\right)\) tại 2 điểm phân biệt
\(\Rightarrow\) Hệ (1) có 6 nghiệm phân biệt (trong đó 3 nghiệm nhỏ hơn \(x_1\) và 3 nghiệm lớn hơn \(x_1\))
Từ đó ta có dấu của y' như sau:

Có 3 lần y' đổi dấu từ dương sang âm nên hàm có 3 cực đại