Giải phương trình cos 2x – 5sin x – 4 =0
![]()
![]()
![]()
![]()
Giải phương trình:
1,\(3sin^22x-2sin2x\times cos2x-4cos^22x=2\)
2,\(2\sqrt{3}cos^2x+6sinx\times cosx=3+\sqrt{3}\)
3,\(3cos^24x+5sin^24x=2-2\sqrt{3}sin4xcos4x\)
1.
\(3sin^22x-2sin2x.cos2x-4cos^22x=2\)
\(\Leftrightarrow-\dfrac{3}{2}\left(1-2sin^22x\right)-2sin2x.cos2x-2\left(2cos^22x-1\right)=\dfrac{5}{2}\)
\(\Leftrightarrow sin4x+\dfrac{7}{2}cos4x=-\dfrac{5}{2}\)
\(\Leftrightarrow\dfrac{\sqrt{53}}{2}\left(\dfrac{2}{\sqrt{53}}sin4x+\dfrac{7}{\sqrt{53}}cos4x\right)=-\dfrac{5}{2}\)
\(\Leftrightarrow sin\left(4x+arccos\dfrac{2}{\sqrt{53}}\right)=-\dfrac{5}{\sqrt{53}}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+arccos\dfrac{2}{\sqrt{53}}=arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+k2\pi\\4x+arccos\dfrac{2}{\sqrt{53}}=\pi-arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{4}arccos\dfrac{2}{\sqrt{53}}+\dfrac{1}{4}arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}-\dfrac{1}{4}arccos\dfrac{2}{\sqrt{53}}-\dfrac{1}{4}arcsin\left(-\dfrac{5}{\sqrt{53}}\right)+\dfrac{k\pi}{2}\end{matrix}\right.\)
2.
\(2\sqrt{3}cos^2x+6sinx.cosx=3+\sqrt{3}\)
\(\Leftrightarrow\sqrt{3}\left(2cos^2x-1\right)+6sinx.cosx=3\)
\(\Leftrightarrow\sqrt{3}cos2x+3sin2x=3\)
\(\Leftrightarrow2\sqrt{3}\left(\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x\right)=3\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k\pi\end{matrix}\right.\)
3.
\(3cos^24x+5sin^24x=2-2\sqrt{3}sin4x.cos4x\)
\(\Leftrightarrow4cos^24x+4sin^24x-cos^24x+sin^24x=2-2\sqrt{3}sin4x.cos4x\)
\(\Leftrightarrow4-cos8x=2-\sqrt{3}sin8x\)
\(\Leftrightarrow cos8x-\sqrt{3}sin8x=2\)
\(\Leftrightarrow\dfrac{1}{2}cos8x-\dfrac{\sqrt{3}}{2}sin8x=1\)
\(\Leftrightarrow cos\left(8x+\dfrac{\pi}{3}\right)=1\)
\(\Leftrightarrow8x+\dfrac{\pi}{3}=k2\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{24}+\dfrac{k\pi}{4}\)
giải phương trình lượng giác
\(2cos^2x-1=sin3x\)
\(2sin^4x-5sin^3x-sin^2x+3sinx+1=0\)
\(sin^6x+cos^6x=2cos^2\left(\frac{\pi}{4}-x\right)\)
a/
\(\Leftrightarrow cos2x=sin3x\)
\(\Leftrightarrow cos2x=cos\left(\frac{\pi}{2}-3x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{2}-3x+k2\pi\\2x=3x-\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{10}+\frac{k2\pi}{5}\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow\left(sinx-1\right)\left(2sinx+1\right)\left(sin^2x-2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\frac{1}{2}\\sinx=1-\sqrt{2}\end{matrix}\right.\) \(\Leftrightarrow x=...\)
c/
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=1+cos\left(\frac{\pi}{2}-2x\right)\)
\(\Leftrightarrow1-3sin^2x.cos^2x=1+sin2x\)
\(\Leftrightarrow-\frac{3}{4}sin^22x=sin2x\)
\(\Leftrightarrow3sin^22x+4sin2x=0\)
\(\Leftrightarrow sin2x\left(3sin2x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\sin2x=-\frac{4}{3}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=\frac{k\pi}{2}\)
Giải các phương trình sau:
1) sin2x + sin23x - 3cos22x = 0
2) sin22x + sin24x = sin26x
3) cos4x - 5sin4x = 1
4) sin24x + sin23x = cos22x +cos2x với x∈(0;π)
5) 4sin3x - 1 = 3 - √3cos3x
6)sin2x = cos22x + cos23x
Gọi S là tập hợp các nghiệm thuộc đoạn - 2 π , 2 π của phương trình
5 sin x + cos 3 x + sin 3 x 1 + 2 sin 2 x = cos 2 x + 3
Giả sử M,m là phần tử lớn nhất và nhỏ nhất của tập hợp S. Tính H=M-m.
A. H = 2 π
B. H = 10 π 3
C. H = 11 π 3
D. H = 7 π 3
Phương trình 2 x 2 + 1 + 3 x 2 + 2 = 5 sin x + cos x có số nghiệm là ?
A. 2
B. 1
C. 0
D. 3
Chọn C.
Ta có ![]()
Mà 5( sinx + cosx) ≤ 5.(1 + 1) = 10
![]() phương trình vô nghiệm.
phương trình vô nghiệm.
Giải phương trình :
cos 2x - cos x - 2 = 0
tìm nghiệm hả anh
nghiệm = 1 đó
giải ra dài dòng lắm anh
Trình bày hẳn ra hộ mik ạ :<
COS(2X) + COS(X) -2=O
TA CÓ CÓS(2X)=(COSX)^2 - (SINX)^2
THAY VÀO TA CÓ:: (COSX)^2 - (SINX)^2+(COSX) -2 =0
<=> (COSX)^2-[1-(COSX)^2)]+COSX-2=0
<=>2.(COSX)^2+COSX-3=O
<=>COSX=1 HOẶC COSX=-3/2
COSX=1=>X=K2π
COSX=-3/2(LOẠI VÌ COSX LUÔN LƠN HƠN HOẶC BẰNG -1 VÀ NHỎ H
1. Giải các phương trình sau:
a) \(\cos\left(x+15^0\right)=\dfrac{2}{5}\)
b) \(\cot\left(2x-10^0\right)=4\)
c) \(\cos\left(x+12^0\right)+\sin\left(78^0-x\right)=1\)
2. Định m để các phương trình sau có nghiệm:
\(\sin\left(3x-27^0\right)=2m^2+m\)
c.
\(\Leftrightarrow cos\left(x+12^0\right)+cos\left(90^0-78^0+x\right)=1\)
\(\Leftrightarrow2cos\left(x+12^0\right)=1\)
\(\Leftrightarrow cos\left(x+12^0\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+12^0=60^0+k360^0\\x+12^0=-60^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=48^0+k360^0\\x=-72^0+k360^0\end{matrix}\right.\)
2.
Do \(-1\le sin\left(3x-27^0\right)\le1\) nên pt có nghiệm khi:
\(\left\{{}\begin{matrix}2m^2+m\ge-1\\2m^2+m\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2m^2+m+1\ge0\left(luôn-đúng\right)\\2m^2+m-1\le0\end{matrix}\right.\)
\(\Rightarrow-1\le m\le\dfrac{1}{2}\)
a.
\(\Rightarrow\left[{}\begin{matrix}x+15^0=arccos\left(\dfrac{2}{5}\right)+k360^0\\x+15^0=-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-15^0+arccos\left(\dfrac{2}{5}\right)+k360^0\\x=-15^0-arccos\left(\dfrac{2}{5}\right)+k360^0\end{matrix}\right.\)
b.
\(2x-10^0=arccot\left(4\right)+k180^0\)
\(\Rightarrow x=5^0+\dfrac{1}{2}arccot\left(4\right)+k90^0\)
2.
Phương trình \(sin\left(3x-27^o\right)=2m^2+m\) có nghiệm khi:
\(2m^2+m\in\left[-1;1\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m^2+m\le1\\2m^2+m\ge-1\end{matrix}\right.\)
\(\Leftrightarrow\left(m+1\right)\left(2m-1\right)\le0\)
\(\Leftrightarrow-1\le m\le\dfrac{1}{2}\)
Giải phương trình: cos 2 x - 3 cos x = 4 cos 2 x 2

![]()


Giải phương trình sau: cos 2x - 3sin x - 2 = 0
![]()
![]()
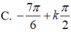
![]()