Phương trình lượng giác 2 cos x + 2 = 0 có nghiệm là:
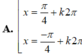
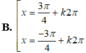
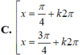
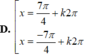
1) cho góc x thỏa mãn \(cosx=-\dfrac{4}{5}\) và \(\pi< x< \dfrac{3\pi}{2}\) tính \(P=tan\left(x-\dfrac{\pi}{4}\right)\)
2) giải phương trình \(2cosx-\sqrt{2}=0\)
3) phương trình lượng giác \(cos3x=cos\dfrac{\pi}{15}\) có nghiệm là
Số điểm biểu diễn cung lượng giác có số đo là nghiệm của phương trình c o t x = tan x + 2 . cos 4 x sin 2 x trên đường tròn lượng giác là
A. 2
B. 3
C. 6
D. 4
a) Giải phương trình \(\cos x = - \frac{1}{2}\)
b) Tìm góc lượng giác x sao cho \(\cos x = \cos \left( { - {{87}^ \circ }} \right)\)
a) \(\cos x = - \frac{1}{2} \Leftrightarrow \cos x = \cos \left( {\frac{{2\pi }}{3}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = - \frac{{2\pi }}{3} + k2\pi \end{array} \right.\)
b) \(\cos x = \cos \left( { - {{87}^ \circ }} \right) \Leftrightarrow \left[ \begin{array}{l}x = - {87^ \circ } + k.360\\x = {87^ \circ } + k{.360^ \circ }\end{array} \right.\)
Tìm nghiệm của phương trình lượng giác cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π
A. x = π 2
B. x=0
C. x= π
D. x=2
Đáp án A
Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
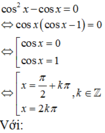
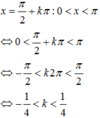
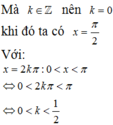
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.
Sai lầm và chú ý: Đối với những bài toán giải phương trình lượng giác thỏa mãn điều kiện cho trước, ta cần tìm được x sau đó cho x thỏa mãn điều kiện đầu bài và cô lập được k khi đó ta sẽ tìm được giá trị nguyên k thỏa mãn và sẽ tìm đc x.
Biểu diễn tập nghiệm của phương trình cos x + cos 2x + cos 3x = 0 trên đường tròn lượng giác ta được số điểm cuối là
A. 6
B. 5
C. 4
D. 2
Giải phương trình lượng giác: \(\cos^23x.\cos2x-\cos^2x=0\)
Giải các phương trình lượng giác sau:
\(\begin{array}{l}a,\,\,sin2x = \;\frac{1}{2}\\b)\;sin(x - \frac{\pi }{7}) = sin\frac{{2\pi }}{7}\\c)\;sin4x - cos\left( {x + \frac{\pi }{6}} \right) = 0\end{array}\)
a) Vì \(\sin \frac{\pi }{6} = \frac{1}{2}\) nên ta có phương trình \(sin2x = \sin \frac{\pi }{6}\)
\( \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{6} + k2\pi \\2x = \pi - \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{12}} + k\pi \\x = \frac{{5\pi }}{{12}} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\(\begin{array}{l}b,\,\,sin(x - \frac{\pi }{7}) = sin\frac{{2\pi }}{7}\\ \Leftrightarrow \left[ \begin{array}{l}x - \frac{\pi }{7} = \frac{{2\pi }}{7} + k2\pi \\x - \frac{\pi }{7} = \pi - \frac{{2\pi }}{7} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3\pi }}{7} + k2\pi \\x = \frac{{6\pi }}{7} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}\;c)\;sin4x - cos\left( {x + \frac{\pi }{6}} \right) = 0\\ \Leftrightarrow sin4x = cos\left( {x + \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{2} - x - \frac{\pi }{6}} \right)\\ \Leftrightarrow sin4x = \sin \left( {\frac{\pi }{3} - x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}4x = \frac{\pi }{3} - x + k2\pi \\4x = \pi - \frac{\pi }{3} + x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{15}} + k\frac{{2\pi }}{5}\\x = \frac{{2\pi }}{9} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Giải phương trình lượng giác :
\(\cos2x-\sin x+\cos x=0\)
\(\cos2x-\sin x+\cos x=0\Leftrightarrow\cos^2x-\sin^2x+\left(\cos x-\sin x\right)=0\)
\(\Leftrightarrow\left(\cos x-\sin x\right)\left(\cos x+\sin x+1\right)=0\)
\(\Leftrightarrow\begin{cases}\cos x-\sin x=0\\\cos x+\sin x+1=0\end{cases}\) \(\Leftrightarrow\begin{cases}\sqrt{2}\cos\left(x+\frac{\pi}{4}\right)=0\\\sqrt{2}\cos\left(x-\frac{\pi}{4}\right)=-1\end{cases}\)
\(\Leftrightarrow\begin{cases}x+\frac{\pi}{4}=\frac{\pi}{2}+k\pi\\x-\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\\x-\frac{\pi}{4}=-\frac{3\pi}{4}+k2\pi\end{cases}\) \(\Leftrightarrow\begin{cases}x=\frac{\pi}{4}+k\pi\\x=\pi+k2\pi\\x=-\frac{\pi}{2}+k2\pi\end{cases}\)
Giải phương trình lượng giác sau :
cos 2x - 3 sin x = 2
Giải phương trình lượng giác
cos 2(x + \(\dfrac{\Pi}{3}\)) +4cos ( \(\dfrac{\Pi}{6}\)-x) =\(\dfrac{5}{6}\)
\(cos2\left(x+\dfrac{\pi}{3}\right)\) là \(cos2\left(x+\dfrac{\pi}{3}\right)\) hay \(cos^2\left(x+\dfrac{\pi}{3}\right)\) vậy bạn?
Số 2 đó là góc nhân đôi hay bình phương?