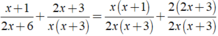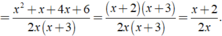Thực hiện phép cộng các phân thức sau:
a) u + 10 u − 2 + u − 18 u − 2 + u + 2 u 2 − 4 với u ≠ ± 1 2 ;
b) 2 − x 2 x 2 y 2 + 5 + 2 y 8 x 3 y 2 + x − 7 4 x 3 y với x ≠ 0 và y ≠ 0 .
Những câu hỏi liên quan
SGK Kết nối tri thức và cuộc sống
22 tháng 7 2023 lúc 9:21
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{a}{{a - 3}} - \dfrac{3}{{a + 3}}\) b) \(\dfrac{1}{{2x}} + \dfrac{2}{{{x^2}}}\) c) \(\dfrac{4}{{{x^2} - 1}} - \dfrac{2}{{{x^2} + x}}\)
`a, a/(a-3) - 3/(a+3) = (a(a+3) - 3(a-3))/(a^2-9)`
`= (a^2+9)/(a^2-9)`
`b, 1/(2x) + 2/x^2 = x/(2x^2) + 4/(2x^2) = (x+4)/(2x^2)`
`c, 4/(x^2-1) - 2/(x^2+x) = (4x)/(x(x-1)(x+1)) - (2(x-1))/(x(x+1)(x-1))`
`= (2x+2)/(x(x-1)(x+1)`
`= 2/(x(x-1))`
Đúng 1
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
22 tháng 7 2023 lúc 9:20
Thực hiện các phép tính cộng, trừ phân thức sau:
a) \(\dfrac{x}{{x + 3}} + \dfrac{{2 - x}}{{x + 3}}\) b) \(\dfrac{{{x^2}y}}{{x - y}} - \dfrac{{x{y^2}}}{{x - y}}\) c) \(\dfrac{{2x}}{{2x - y}} + \dfrac{y}{{y - 2x}}\)
\(a,\dfrac{x}{x+3}+\dfrac{2-x}{x+3}\\ =\dfrac{x+2-x}{x+3}\\ =\dfrac{2}{x+3}\\b,\dfrac{x^2y}{x-y}-\dfrac{xy^2}{x-y}\\ =\dfrac{x^2y-xy^2}{x-y}\\ =\dfrac{xy\left(x-y\right)}{x-y}\\ =xy\\ c,\dfrac{2x}{2x-y}+\dfrac{y}{y-2x}\\=\dfrac{2x}{2x-y}-\dfrac{y}{2x-y}\\ =\dfrac{2x-y}{2x-y}\\ =1 \)
Đúng 1
Bình luận (0)
`a, x/(x+3) + (2-x)/(x+3) = (x+2-x)/(x+3) = 2/(x+3)`
`b, (x^2y)/(x-y) - (xy^2)/(x-y) = (x^2y-xy^2)/(x-y) = (xy(x-y))/(x-y)= xy`
`c, (2x)/(2x-y) - (y)/(2x-y)`
`= (2x-y)/(2x-y) = 1`
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
22 tháng 7 2023 lúc 9:25
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{{a - 1}}{{a + 1}} + \dfrac{{3 - a}}{{a + 1}}\) b) \(\dfrac{b}{{a - b}} + \dfrac{a}{{b - a}}\) c) \(\dfrac{{{{\left( {a + b} \right)}^2}}}{{ab}} - \dfrac{{{{\left( {a - b} \right)}^2}}}{{ab}}\)
a) \(\dfrac{a-1}{a+1}+\dfrac{3-a}{a+1}\)
\(=\dfrac{a-1+3-a}{a+1}\)
\(=\dfrac{2}{a+1}\)
b) \(\dfrac{b}{a-b}+\dfrac{a}{b-a}\)
\(=\dfrac{b}{a-b}+\dfrac{-a}{a-b}\)
\(=\dfrac{b-a}{a-b}\)
\(=-1\)
c) \(\dfrac{\left(a+b\right)^2}{ab}-\dfrac{\left(a-b\right)^2}{ab}\)
\(=\dfrac{\left[\left(a+b\right)-\left(a-b\right)\right]\left[\left(a+b\right)+\left(a-b\right)\right]}{ab}\)
\(=\dfrac{4ab}{ab}\)
\(=4\)
Đúng 1
Bình luận (0)
`a, (a-1)/(a+1) + (3-a)/(a+1)`
`= (a-1+3-a)/(a+1)`
`=2/(a+1)`
`b, b/(a-b) + a/(b-a)`
`= b/(a-b) - a/(a-b)`
`= (b-a)/(a-b)`
`c, (a+b)^2/(ab) -(a-b)^2/(ab)`
`=(a^2+2ab+b^2-a^2+2ab-b^2)/(ab)`
`= (4ab)/(ab)`
Đúng 0
Bình luận (4)
SGK Kết nối tri thức và cuộc sống
22 tháng 7 2023 lúc 9:25
Thực hiện các phép cộng, trừ phân thức sau:
a) \(\dfrac{1}{{2a}} + \dfrac{2}{{3b}}\)
b) \(\dfrac{{x - 1}}{{x + 1}} - \dfrac{{x + 1}}{{x - 1}}\)
c) \(\dfrac{{x + y}}{{xy}} - \dfrac{{y + z}}{{yz}}\)
d) \(\dfrac{2}{{x - 3}} - \dfrac{{12}}{{{x^2} - 9}}\)
e) \(\dfrac{1}{{x - 2}} + \dfrac{2}{{{x^2} - 4x + 4}}\)
a: \(=\dfrac{3b+4a}{6ab}\)
b: \(=\dfrac{x^2-2x+1-x^2-2x-1}{x^2-1}=\dfrac{-4x}{x^2-1}\)
c: \(=\dfrac{xz+yz-xy-xz}{xyz}=\dfrac{yz-xy}{xyz}=\dfrac{z-x}{xz}\)
d: \(=\dfrac{2x+6-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
e: \(=\dfrac{x-2+2}{\left(x-2\right)^2}=\dfrac{x}{\left(x-2\right)^2}\)
Đúng 1
Bình luận (0)
Thực hiện phép trừ các phân thức sau: a)
5
u
+
u
u
+
6
−
30
u
2
+
6
u
với
u
≠
−
6
và
u
≠
0
b)
3
p...
Đọc tiếp
Thực hiện phép trừ các phân thức sau:
a) 5 u + u u + 6 − 30 u 2 + 6 u với u ≠ − 6 và u ≠ 0
b) 3 p + 1 ( p − 1 ) 2 − 1 p + 1 + p + 3 1 − p 2 với p ≠ ± 1 .
Thực hiện phép nhân các phân thức sau:a)
2
u
2
−
20
u
+
50
5
u
+
5
.
2
u
2
−
2
4...
Đọc tiếp
Thực hiện phép nhân các phân thức sau:
a) 2 u 2 − 20 u + 50 5 u + 5 . 2 u 2 − 2 4 ( u − 5 ) 3 với u ≠ ± 5 ;
b) v + 3 v 2 − 4 . 8 − 12 v + 6 v 2 − v 3 7 v + 21 với v ≠ − 3 và v ≠ ± 2 .
a) Ta có 2 u 2 − 20 u + 50 5 u + 5 . 2 u 2 − 2 4 ( u − 5 ) 3 = 2 ( u − 5 ) 2 5 ( u + 1 ) . 2 ( u − 1 ) ( u + 1 ) 4 ( u − 5 ) 3 = u − 1 5 ( u − 5 )
b) Ta có v + 3 v 2 − 4 . 8 − 12 v + 6 v 2 − v 3 7 v + 21 = v + 3 ( v − 2 ) ( v + 2 ) . ( 2 − v ) 3 7 ( v + 3 ) = 1 ( v − 2 ) ( v + 2 ) . − ( v − 2 ) 3 7 = − ( v − 2 ) 2 7 ( v + 2 )
Đúng 0
Bình luận (0)
Thực hiện phép cộng các phân thức sau x 2 + x 4 + 1 1 - x 2 + 1
Thực hiện phép cộng các phân thức sau: x 2 + x 4 + 1 1 - x 2 + 1
Thực hiện phép cộng các phân thức sau: x + 1 2 x + 6 + 2 x + 3 x ( x + 3 )
Ta có: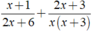
+
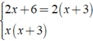⇒ MTC = 2x( x + 3 )
Khi đó ta có:
Đúng 0
Bình luận (0)