Bất phương trình mx > 3 + m vô nghiệm khi:
A. m = 0
B. m > 0
C. m < 0
D. m ≠ 0
Những câu hỏi liên quan
Bất phương trình mx\(^2\)+2(m+3)x+m+1\(\ge\)0 vô nghiệm khi và chỉ khi
Cho hệ bất phương trình
mx
+
2
m
0
2
x
+
3
5...
Đọc tiếp
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R
(III) Khi m≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là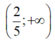 
(IV) Khi m> 0 thì hệ bất phương trình đã cho có tập nghiệm là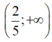 
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Cho hệ bất phương trình
mx
+
2
m
0
2
x
+
3
5...
Đọc tiếp
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R.
(III) Khi m ≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
(IV) Khi m > 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Tìm m để bất phương trình x2-mx+m+3<0 vô nghiệm
BPT đã cho vô nghiệm khi và chỉ khi: \(x^2-mx+m+3\ge0\) nghiệm đúng với mọi x
\(\Rightarrow\left\{{}\begin{matrix}a=1>0\\\Delta=m^2-4\left(m+3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow m^2-4m-12\le0\)
\(\Rightarrow-2\le m\le6\)
Đúng 2
Bình luận (0)
Bài 3. Xác định m để hệ bất phương trình sau có nghiệm, vô nghiệm, có nghiệm duy nhất?a)left{{}begin{matrix}x+m-103m-2-x0end{matrix}right. b)left{{}begin{matrix}x-10mx-30end{matrix}right. c)left{{}begin{matrix}x+4m^2le2mx+13x+22x-1end{matrix}right.d)left{{}begin{matrix}7x-2ge-4x+192x-3m+2 0end{matrix}right. e)left{{}begin{matrix}mx-10left(3m-2right)x-m0end{matrix}right.
Đọc tiếp
Bài 3. Xác định m để hệ bất phương trình sau có nghiệm, vô nghiệm, có nghiệm duy nhất?a)\(\left\{{}\begin{matrix}x+m-1>0\\3m-2-x>0\end{matrix}\right.\) b)\(\left\{{}\begin{matrix}x-1>0\\mx-3>0\end{matrix}\right.\) c)\(\left\{{}\begin{matrix}x+4m^2\le2mx+1\\3x+2>2x-1\end{matrix}\right.\)
d)\(\left\{{}\begin{matrix}7x-2\ge-4x+19\\2x-3m+2< 0\end{matrix}\right.\) e)\(\left\{{}\begin{matrix}mx-1>0\\\left(3m-2\right)x-m>0\end{matrix}\right.\)
Tìm m để hệ bất phương trình : có nghiệm, vô nghiệm, có nghiệm duy nhất .a) left{{}begin{matrix}x+m-103m-2-x0end{matrix}right.b) left{{}begin{matrix}x-10mx-30end{matrix}right.c) left{{}begin{matrix}x+4m^2le2mx+13x+22x-1end{matrix}right.d) left{{}begin{matrix}7x-2ge-4x+192x-3m+2 0end{matrix}right.e) left{{}begin{matrix}mx-10left(3m-2right)x-m0end{matrix}right.MỌI NGƯỜI ƠI GIÚP EM VỚI GẤP LẮM RỒI
Đọc tiếp
Tìm m để hệ bất phương trình : có nghiệm, vô nghiệm, có nghiệm duy nhất .
a) \(\left\{{}\begin{matrix}x+m-1>0\\3m-2-x>0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x-1>0\\mx-3>0\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}x+4m^2\le2mx+1\\3x+2>2x-1\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}7x-2\ge-4x+19\\2x-3m+2< 0\end{matrix}\right.\)
e) \(\left\{{}\begin{matrix}mx-1>0\\\left(3m-2\right)x-m>0\end{matrix}\right.\)
MỌI NGƯỜI ƠI GIÚP EM VỚI GẤP LẮM RỒI
Tên vietjack mà không làm được thì mang tiếng người ta quá
Đúng 0
Bình luận (5)
a, Hệ ⇔ \(\left\{{}\begin{matrix}x>1-m\\x< 3m-2\end{matrix}\right.\)
Hệ không thể có nghiệm duy nhất
Hệ có nghiệm khi \(\left(1-m;+\infty\right)\cap\left(-\infty;3m-2\right)\ne\varnothing\)
⇔ 3m - 2 > 1 - m
⇔ m > \(\dfrac{4}{3}\)
Vậy hệ vô nghiệm khi m ≤ \(\dfrac{4}{3}\)
Đúng 0
Bình luận (0)
Tìm m để phương trình:
a) x^2 – 2mx + m + 6 = 0 có hai nghiệm phân biệt.
b) mx^2 – 2mx + m + 3 = 0 vô nghiệm.
c) (m – 2)x^2 + (2m – 3)x + m +1 = 0 có nghiệm kép
a, Để pt có 2 nghiệm pb khi \(\Delta>0\)
\(\Delta=\left(-2m\right)^2-4\left(m+6\right)=4m^2-4m-24>0\Leftrightarrow m< -2;m>3\)
b, Để pt trên là pt bậc 2 khi \(m\ne0\)
Để pt vô nghiệm khi \(\Delta< 0\)
\(\Delta=4m^2-4m\left(m+3\right)=4m^2-4m^2-12m< 0\Leftrightarrow-12m< 0\Leftrightarrow m>0\)
c, Để pt trên là pt bậc 2 khi \(m\ne2\)
Để pt trên có nghiệm kép \(\Delta=0\)
\(\Delta=\left(2m-3\right)^2-4\left(m+1\right)\left(m-2\right)=4m^2-12m+9-4\left(m^2-m-2\right)\)
\(=-8m+17=0\Leftrightarrow m=\frac{17}{8}\)
mx²+2(m-1)x+4 ≥0 tìm m để bất phương trình vô nghiệm
mx²+2(m-1)x+4 ≥0
bpt trên vô nghiệm <=>mx²+2(m-1)x+4 <0
a=m\(\ne0\)
\(\Delta'=\left(m-1\right)^2-m.4\)
\(=m^2-2m+1-4m\)
\(=m^2-6m+1\)
\(=\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)\)
bpt vô nghiệm <=>\(\left\{{}\begin{matrix}a< 0\\\Delta'< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\3-2\sqrt{2}< m< 3+2\sqrt{2}\end{matrix}\right.\)
=> không có m để bất phương trình vô nghiệm
Đúng 2
Bình luận (0)
Tìm tham số m để hệ bất phương trình sau : 1)có nghiệm 2)vô nghiệm a) left{{}begin{matrix}x+m-103m-2-x0end{matrix}right.b) left{{}begin{matrix}x-10mx-30end{matrix}right.c) left{{}begin{matrix}x+4m^2le2mx+13x+22x-1end{matrix}right.d) left{{}begin{matrix}7x-2ge-4x+192x-3m+2 0end{matrix}right.e) left{{}begin{matrix}mx-10left(3m-2right)x-m0end{matrix}right.
Đọc tiếp
Tìm tham số m để hệ bất phương trình sau : 1)có nghiệm 2)vô nghiệm
a) \(\left\{{}\begin{matrix}x+m-1>0\\3m-2-x>0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x-1>0\\mx-3>0\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}x+4m^2\le2mx+1\\3x+2>2x-1\end{matrix}\right.\)
d) \(\left\{{}\begin{matrix}7x-2\ge-4x+19\\2x-3m+2< 0\end{matrix}\right.\)
e) \(\left\{{}\begin{matrix}mx-1>0\\\left(3m-2\right)x-m>0\end{matrix}\right.\)
Tìm m để phương trình \(mx^2+2\left(m-1\right)x+m+3=0\)
a) có nghiệm kép; b) có hai nghiệm phân biệt;
c) có nghiệm; d) vô nghiệm.
\(mx^2+2\left(m-1\right)x+m+3=0\)(Đk:m≠0)
\(\Delta'=\left(m-1\right)^2-m\left(m+3\right)\)
\(\Delta'=m^2-2m+1-m^2-3m\)
\(\Delta'=1-5m\)
a,Để pt có nghiệm kép
Thì\(\Delta'=0\)
\(\Leftrightarrow1-5m=0\Rightarrow m=\dfrac{1}{5}\)
b, Để pt có 2 nghiệm phân biệt
Thì\(\Delta'>0\)
\(\Leftrightarrow1-5m>0\Rightarrow m< \dfrac{1}{5}\)
c,Để pt có nghiệm
Thì\(\Delta'\ge0\)
\(\Leftrightarrow1-5m\ge0\Rightarrow m\le\dfrac{1}{5}\)
d, Để pt vô nghiệm
Thì\(\Delta'< 0\)
\(\Leftrightarrow1-5m< 0\Rightarrow m>\dfrac{1}{5}\)
Đúng 2
Bình luận (0)
Lời giải:
$m=0$ thì pt trở thành $-2x+3=0\Leftrightarrow x=\frac{3}{2}$
$m\neq 0$ thì pt là pt bậc 2 ẩn $x$
$\Delta'=(m-1)^2-m(m+3)=1-5m$
PT có nghiệm kép $\Leftrightarrow \Delta'=1-5m=0\Leftrightarrow m=\frac{1}{5}$
PT có 2 nghiệm pb $\Leftrightarrow \Delta'=1-5m>0$
$\Leftrightarrow m< \frac{1}{5}$
Vậy pt có 2 nghiệm pb khi $m< \frac{1}{5}$ và $m\neq 0$
PT có nghiệm khi \(\left[\begin{matrix} m=0\\ \Delta'=1-5m\geq 0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} m=0\\ m\leq \frac{1}{5}\end{matrix}\right.\Leftrightarrow m\leq \frac{1}{5}\)
PT vô nghiệm khi $\Delta'=1-5m< 0$
$\Leftrightarrow m> \frac{1}{5}$
Đúng 4
Bình luận (0)
Ta có: \(\Delta=\left[2\left(m-1\right)\right]^2-4\cdot m\cdot\left(m+3\right)\)
\(=\left(2m-2\right)^2-4m\left(m+3\right)\)
\(=4m^2-8m+4-4m^2-12m\)
\(=-16m+4\)
a) Để phương trình có nghiệm kép thì \(\Delta=0\)
\(\Leftrightarrow-16m=-4\)
hay \(m=\dfrac{1}{4}\)
b) Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Leftrightarrow-16m>-4\)
hay \(m< \dfrac{1}{4}\)
c) Để phương trình có nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow-16m\ge-4\)
hay \(m\le\dfrac{1}{4}\)
Đúng 1
Bình luận (0)