Phân thức x x + 3 xác định khi
A. x = -3
B. x ≠ 3
C. x ≠ 0
D. x ≠ -3
Cho biểu thức \(A=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}-\dfrac{3\sqrt{x}-2}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
a) Tìm điều kiện xác định của \(A\)
b) Tính giá trị của biểu thức \(A\) khi \(x=0\)
c) Rút gọn biểu thức \(A\)
d) Tìm \(x\) để \(A=-\dfrac{8}{5}\)
e) Tìm \(x\) để \(A=\sqrt{x}-\dfrac{18}{5}\)
f) Tìm điều kiện của \(x\) để \(A< 0\)
g) Tìm điều kiện của \(x\) để \(A>0\)
h) Tìm tập hợp các số tự nhiên \(x\) để \(A>0\)
k) Chứng minh rằng \(A>-5\)
m) Tìm điều kiện của \(x\) để\(A>-3\)
n*) Tìm giá trị lớn nhất của biểu thức \(A\)
p*) Xét biểu thức \(M=A-\dfrac{27}{\sqrt{x}+3}\). Tìm giá trị nhỏ nhất của biểu thức \(M\)
q*) Tìm các số tự nhiên \(x\) để \(A\) là số nguyên
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b) Thay x=0 vào A, ta được:
\(A=\dfrac{15\cdot\sqrt{0}-11}{0+2\sqrt{0}-3}-\dfrac{3\sqrt{0}-2}{\sqrt{0}-1}-\dfrac{2\sqrt{0}+3}{\sqrt{0}+3}\)
\(=\dfrac{-11}{-3}-\dfrac{-2}{-1}-\dfrac{3}{3}\)
\(=\dfrac{11}{3}-2-1\)
\(=\dfrac{11}{3}-\dfrac{9}{3}=\dfrac{2}{3}\)
1.Cho biểu thức C = x³/x²-4 - x/x-2 - 2/x+2
a,tìm giá trị của biến để biểu thức được xác định
b,Tìm x để C=0
c,Tìm giá trị nguyên của x để C nhận giá trị dương
2,cho P = (2+x/2-x + 4x²/x²-4 - 2-x/2+x): x²-3x/2x²-x³
a,Tìm điều kiện của x để giá trị của P được xác định
B, rút gọn P
c,Tính giá trị P với |x-5|=2
d,Tìm x để P<0
3,cho biểu thức B = [x+1/2x-2 + 3/x²-1 - x+3/2x+2]. 4x²-4/5
a,Tìm điều kiện của x để giá trị biểu thức được xác định
b,CMR khi giá trị của biểu thức không phụ thuộc vào giá trị của biến x?
4,Cho phân thức C = 3x²-x/9x²-6x+1
a, tìm điều kiện xác định phân thức
b,tính giá trị phân thức tại x=-8
c,Tìm x để giá trị của phân thức nhận giá trị dương
1.a)\(\frac{x^3}{x^2-4}-\frac{x}{x-2}-\frac{2}{x+2}\)
\(=\frac{x^3}{\left(x+2\right)\left(x-2\right)}-\frac{x}{x-2}-\frac{2}{x+2}\)
Để biểu thức được xác định thì:\(\left(x+2\right)\left(x-2\right)\ne0\)\(\Rightarrow x\ne\pm2\)
\(\left(x+2\right)\ne0\Rightarrow x\ne-2\)
\(\left(x-2\right)\ne0\Rightarrow x\ne2\)
Vậy để biểu thức xác định thì : \(x\ne\pm2\)
b) để C=0 thì ....
1, c , bn Nguyễn Hữu Triết chưa lm xong
ta có : \(/x-5/=2\)
\(\Rightarrow\orbr{\begin{cases}x-5=2\\x-5=-2\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=3\end{cases}}\)
thay x = 7 vào biểu thứcC
\(\Rightarrow C=\frac{4.7^2\left(2-7\right)}{\left(7-3\right)\left(2+7\right)}=\frac{-988}{36}=\frac{-247}{9}\)KL :>...
thay x = 3 vào C
\(\Rightarrow C=\frac{4.3^2\left(2-3\right)}{\left(3-3\right)\left(3+7\right)}\)
=> ko tìm đc giá trị C tại x = 3
chết mk nhìn nhầm phần c bài 2 :
\(2,\left(\frac{2+x}{2-x}+\frac{4x^2}{x^2-4}-\frac{2-x}{2+x}\right):\frac{x^2-3x}{2x^2-x^3}\)
Để P xác định
\(\Rightarrow2-x\ne0\Rightarrow x\ne2\)
\(2+x\ne0\Rightarrow x\ne-2\)
\(x^2-4\ne0\Rightarrow x\ne0\)
\(x^2-3x\ne0\Rightarrow x\ne3\)
b, \(P=\left(\frac{2+x}{2-x}+\frac{4x^2}{\left(2+x\right)\left(2-x\right)}+\frac{2-x}{2+x}\right):\frac{x\left(x-3\right)}{x^2\left(2-x\right)}\)
\(P=\left[\frac{4+4x+x^2}{\left(2-x\right)\left(2+x\right)}-\frac{4x^2}{\left(2+x\right)\left(2-x\right)}-\frac{4-4x+x^2}{\left(2+x\right)\left(2-x\right)}\right].\frac{x\left(2-x\right)}{x-3}\)
\(P=\left[\frac{8x-4x^2}{\left(2-x\right)\left(2+x\right)}\right].\frac{x\left(2-x\right)}{x-3}=\frac{4x\left(2-x\right)}{\left(2-x\right)\left(2+x\right)}.\frac{x\left(2-x\right)}{x-3}\)
\(P=\frac{4x^2\left(2-x\right)}{\left(x-3\right)\left(2+x\right)}\)
d, ĐỂ \(p=\frac{8x^2-4x^3}{x^2-x-6}< 0\)
\(TH1:8x^2-4x^3< 0\)
\(\Rightarrow8x^2< 4x^3\)
\(\Rightarrow2< x\Rightarrow x>2\)
\(TH2:x^2-x-6< 0\Rightarrow x^2< x+6\)
x^5+x^4-16x-16/x^3-6x^2-9x+14
a)Tìm điều kiện của x để giá trị các phân thức được xác định
b)Rút gọn phân thức
c)Tìm giá trị của x để giá trị của phân thức bằng 0
d)Tìm giá trị của phân thức A tại x=3
Cho phân thức: P=(2x^2+2x)(x-3)^2/x(x^2-9)(x+1)
a)Tìm tập xác định của phân thức P
b)Rút gọn và tính giá trị của P khi x=0,5
c)Tìm x sao cho P=0
\(\frac{\left(2x^2+2x\right)\left(x-3\right)^2}{x\left(x^2-9\right)\left(x+1\right)}.ĐKXD:x\ne3,x\ne0,x\ne-1\)
\(=\frac{2x\left(x+1\right)\left(x-3\right)\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)\left(x+1\right)}=\frac{2x\left(x-3\right)}{x\left(x+3\right)}\)
\(=\frac{2x-6}{x+3}\)
b) Với x=0,5=>\(P=\frac{-5}{3,5}\)
\(P=0\Leftrightarrow2x-6=0\Leftrightarrow x=3\)
cho biểu thức B=[ x+1/ 2x-2 +3/x2 -1 -x+3/2x+2] .2x2 -2/5
a, tìm điều kiện của biến để phân thức xác định
b, c/m rằng khi giá trị của biểu thức xác định thì nó không phụ thuộc vào biến x ?
cho phân thức:A=2x-1\x^2-x
a,tìm điều kiện để giá trị của phân thức được xác định
b,tính giá trị của phân thức khi x=0 và khi x=3
a,x^2- x # 0
hay x(x -1) # 0
<=> ĐKXĐ: x# 0
x -1 #0 => X# 1
bthay x= 0 vào A ta có
A= 2.0-1/ 0^2-0= -1
thay x= 3 vào A ta có
A= 2.3 -1/ 3^2-3 = 5/6
Cho phân thức A= x²+8x+16/ x²-16 a) Tìm điều kiện xác định của A. b) Rút gọn phân thức. c) Tìm giá trị của x để phân thức A có giá trị bằng 3. d ) Có giá trị nào của x để giá trị của phân thức A bằng 0 hay không? Tại sao?
Lời giải:
a. ĐKXĐ: $x^2-16\neq 0\Leftrightarrow (x-4)(x+4)\neq 0$
$\Leftrightarrow x\neq \pm 4$
b. $A=\frac{x^2+8x+16}{x^2-16}=\frac{(x+4)^2}{(x-4)(x+4)}=\frac{x+4}{x-4}$
c. $A=3\Leftrightarrow \frac{x+4}{x-4}=3$
$\Rightarrow x+4=3(x-4)$
$\Leftrightarrow -2x+16=0$
$\Leftrightarrow x=8$ (tm)
d.
$A=0\Leftrightarrow \frac{x+4}{x-4}=0\Leftrightarrow x+4=0\Leftrightarrow x=-4$
Mà theo ĐKXĐ thì $x\neq \pm 4$ nên không tồn tại $x$ để $A=0$
Với Giá trị nào của x thì phân thức 3x+2/3x-2 xác định ?
A. x không bằng -2/3
B. x=2/3
C. x không bằng +- 2/3
D. x không bằng 2/3
(64-^3):(x^2 +4x +16) ta được kết quả là :
A. x+4
B. x -4
C. -(x+4)
D.4-x
Bài 1: Tìm x; biết:
a) 2x^2-8x=0 b) (x+2)^2-x(x-1)=10 c)b x^3-6x^2+9x=0
Bài 2: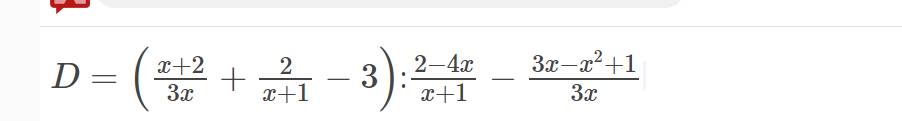
a) Viết điều kiện xác định của biểu thức D
b) Rút gọn biểu thức D
c) Tính giá trị của D khi x=1/
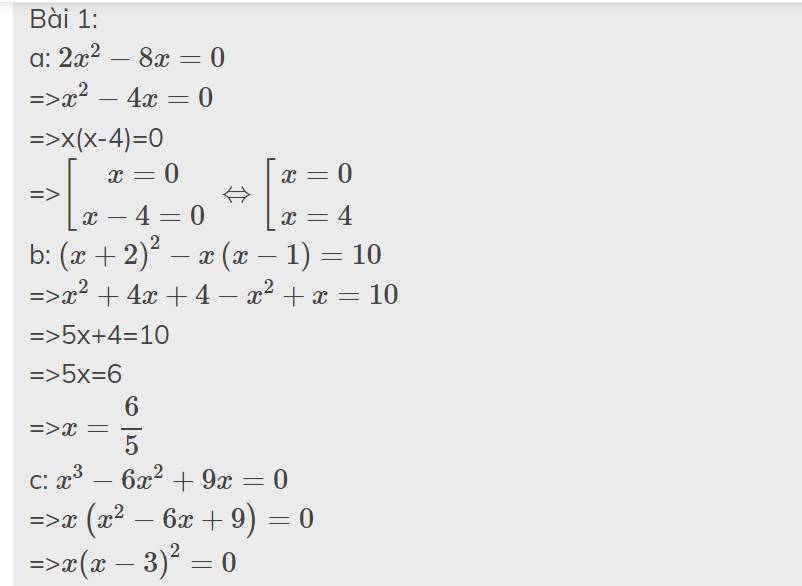
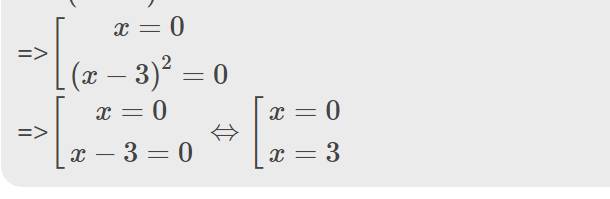 Bài 2:
Bài 2:
a: ĐKXĐ: \(x\notin\left\{0;-1;\dfrac{1}{2}\right\}\)
b: \(D=\left(\dfrac{x+2}{3x}+\dfrac{2}{x+1}-3\right):\dfrac{2-4x}{x+1}-\dfrac{3x-x^2+1}{3x}\)
\(=\dfrac{\left(x+2\right)\left(x+1\right)+6x-3\cdot3x\left(x+1\right)}{3x\left(x+1\right)}\cdot\dfrac{x+1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{x^2+3x+2+6x-9x^2-9x}{3x}\cdot\dfrac{1}{2-4x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-8x^2+2}{3x}\cdot\dfrac{1}{-4x+2}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{-2\left(2x-1\right)\left(2x+1\right)}{3x\cdot\left(-2\right)\left(2x-1\right)}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1}{3x}+\dfrac{x^2-3x-1}{3x}\)
\(=\dfrac{2x+1+x^2-3x-1}{3x}=\dfrac{x^2-x}{3x}=\dfrac{x-1}{3}\)
c: Khi x=1 thì \(D=\dfrac{1-1}{3}=0\)
câu 53:điều kiện để phân thức \(\dfrac{7x^2-x}{x^2-9}\) được xác định khi :
a.\(x\ne3\) b,\(x\ne9\) c,\(x\ne3;x\ne-3\) d,\(x\ne-9vàx\ne9\)
GIẢI THÍCH VÌ SAO LẠI RA KẾT QUẢ ĐÓ
Phân thức `(7x^2 - x)/(x^2 - 9)` được xác đinh khi
`x^2-9≠0`
`(x-3).(x+3)≠0`
`=> x≠3; x ≠ -3`
`=> C`