Cho phân thức 2 x - 1 , nhân cả tử và mẫu với đa thức ( x + 1 ) ta được phân thức mới là ?
A. 2 ( x - 1 ) x 2 - 1
B. 2 ( x + 1 ) x - 1 2
C. 2 ( x + 1 ) x 2 - 1
D. 2 ( x + 1 ) 2 x 2 - 1
Những câu hỏi liên quan
Cho phân thức
2
(
x
-
1
)
, nhân cả tử và mẫu với đa thức ( x + 1 ) ta được phân thức mới là ? A.
2
(
x
-
1
)
x
2
-
1
B. ...
Đọc tiếp
Cho phân thức 2 ( x - 1 ) , nhân cả tử và mẫu với đa thức ( x + 1 ) ta được phân thức mới là ?
A. 2 ( x - 1 ) x 2 - 1
B. 2 ( x - 1 ) 2 x 2 - 1
C. 2 ( x + 1 ) x 2 - 1
D. 2 ( x + 1 ) 2 x 2 - 1
Cho phân thức ( 2 x ) ( x + 2 ) . Nhân cả tử và mẫu với đa thức ( x - 1 ), so sánh phân thức nhận được với phân thức đã cho ?
Ta có phân thức mới là
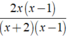
Ta có
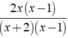
= (2x)/(x + 2)
vì 2x( x - 1 ).( x + 2 ) = 2x.( x + 2 )( x - 1 ).
Đúng 0
Bình luận (0)
Ta có phân thức x x + 1 . Đổi dấu cả tử và mẫu ta được phân thức mới, so sánh phân thức mới với phân thức đã cho
Hướng dẫn:
Ta có phân thức mới nhận được là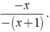
.
Ta có: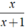
=
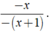vì x. - ( x + 1 ) = - x.( x + 1 ).
Đúng 0
Bình luận (0)
Cho phân thức x/3. Hãy nhân tử và mẫu của phân thức này với x + 2 rồi so sánh phân thức vừa nhận được với phân thức đã cho.
x.(x + 2) = x2 + 2x
3.(x +2) = 3x + 6
⇒ x(3x + 6) = 3(x2 + 2x) = 3x2 + 6x
Đúng 0
Bình luận (0)
16 tháng 11 2021 lúc 13:11
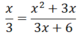
Cho phân thức x/3. Hãy nhân tử và mẫu của phân thức này với x+2 rồi so sánh phân thức vừa nhận được với phân thức đã cho
Phân thức nhận được bằng phân thức đã cho
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử -8 - Phân tích đa thức thành nhân tử -8 x mũ 3 cộng 1 ta được
\(-8x^3+1=1^3-\left(2x\right)^3=\left(1-2x\right)\left(1+2x+4x^2\right)\)
Đúng 1
Bình luận (0)
Tử và mẫu của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)có nhân tử chung là x−1. Viết phân thức nhận được sau khi chia cả tử và mẫu của phân thức này cho nhân tử chung đó. So sánh phân thức mới nhận được với phân thức đã cho.
Chia cả tử và mẫu của phân thức này cho nhân tử chung x−1, ta có \(\frac{{x + 1}}{{{x^2} + x + 1}}\)
=> Phân thức mới được rút gọn và mất đi nhân tử chung x−1
Đúng 0
Bình luận (0)
SGK Cánh Diều trang 33
19 tháng 7 2023 lúc 13:29
Cho hai phân thức \(\dfrac{1}{{{x^2}y}}\) và \(\dfrac{1}{{x{y^2}}}\)
a) Hãy nhân cả tử và mẫu của phân thức thứ nhất với y và nhân cả tử và mẫu của phân thức thứ hai với x.
b) Nhân xét gì về mẫu của hai phân thức thu được.
a) Ta có:
\(\dfrac{1}{{{x^2}y}} = \dfrac{{1.y}}{{{x^2}y.y}} = \dfrac{y}{{{x^2}{y^2}}}\)
\(\dfrac{1}{{x{y^2}}} = \dfrac{{1.x}}{{x{y^2}.x}} = \dfrac{x}{{{x^2}{y^2}}}\)
b) Mẫu của hai phân thức thu được giống nhau đều là: \({x^2}{y^2}\)
Đúng 0
Bình luận (0)
Chia cả tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn
Ta có: \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{2{\rm{x}}}}{{x + 1}}\)
Đúng 0
Bình luận (0)