a) Thay x = 15 ta được:

P = (-35).x - (-15).37 = (-35).15 - (-15).37

   = (-35).15 + 15.37 = 15.[(-35) +37] = 15.2 = 30.

b) Thay x = -37 ta được:

P = (-35).(-37) - (-15).37 = 35.37 + 15.37

   = 37.(15 + 35) = 37.50 = 1850.

a) Thay x = - 8 => 2 . (- 8) = - (2 . 8) = - 16.

b) Thay y = 6 => (- 7) . 6 = - (7 . 6) = - 36.

c) Thay z = - 4 => – 8 . (- 4)  – 15 = - (8 . 4) – 15 = 32 – 15 = 17.

a) x=-16

b) y= -42

c) z=17

a) Thay x=-8 vào biểu thức 2x, ta được:

\(2\cdot\left(-8\right)=-16\)

b) Thay y=6 vào biểu thức -7y, ta được:

\(-7\cdot6=-42\)

c) Thay z=-4 vào biểu thức -8z-15, ta được:

\(\left(-8\right)\cdot\left(-4\right)-15=32-15=17\)

1: Ta có: \(P=\dfrac{x-\sqrt{x}}{x-9}+\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3}\)

\(=\dfrac{x-\sqrt{x}+\sqrt{x}-3-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x-\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\)

2)

a) Thay \(x=\dfrac{9}{4}\) vào P, ta được:

\(P=\left(\dfrac{3}{2}+2\right):\left(\dfrac{3}{2}+3\right)=\dfrac{7}{2}:\dfrac{11}{2}=\dfrac{7}{11}\)

b) Ta có: \(x=\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)

\(=5+\sqrt{2}-4-\sqrt{2}\)

=1

Thay x=1 vào P, ta được:

\(P=\dfrac{1+2}{1+3}=\dfrac{3}{4}\)

Rút gọn biểu thức:

A = (x2 – 5)(x + 3) + (x + 4)(x – x2)

   = x2.(x + 3) + (–5).(x + 3) + x.(x – x2) + 4.(x – x2)

   = x2.x + x2.3 + (–5).x + (–5).3 + x.x + x.(–x2) + 4.x + 4.(–x2)

   = x3 + 3x2 – 5x – 15 + x2 – x3 + 4x – 4x2

   = (x3 – x3) + (3x2 + x2 – 4x2) + (4x – 5x) – 15

   = –x – 15.

a) Nếu x = 0 thì A = –0 – 15 = –15

b) Nếu x = 15 thì A = –15 – 15 = –30

c) Nếu x = –15 thì A = –(–15) – 15 = 15 – 15 = 0

d) Nếu x = 0,15 thì A = –0,15 – 15 = –15,15

ĐKXĐ: x<=4

a: Thay x=-5 vào A, ta được:

\(A=2\cdot\left(-5\right)+3\cdot\sqrt{4+5}+1=-10+1+3\cdot3=0\)

b: Vì x=5 không thỏa mãn ĐKXĐ nên khi x=5 thì A không có giá trị

Tham khảo:

a) \(f\left( x \right) =  - 3{x^2} + 4x - 1\)

\(a =  - 3 < 0\), \(\Delta  = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)

=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)

Bảng xét dấu:

b) \(f\left( x \right) = {x^2} - x - 12\)

\(a = 1 > 0\), \(\Delta  = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)

=> \(f\left( x \right)\) có 2 nghiệm \(x =  - 3,x = 4\)

Bảng xét dấu:

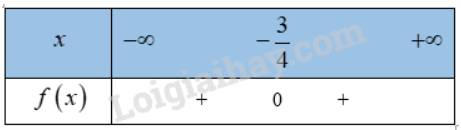
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)

\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)

=> \(f\left( x \right)\) có nghiệm duy nhất \(x =  - \frac{3}{4}\)

Bảng xét dấu:

2:

\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)

\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)

B=(x1+x2)^2-2x1x2

=3^2-2*(-7)

=9+14=23

C=căn (x1+x2)^2-4x1x2

=căn 3^2-4*(-7)=căn 9+28=căn 27

D=(x1^2+x2^2)^2-2(x1x2)^2

=23^2-2*(-7)^2

=23^2-2*49=431

D=9x1x2+3(x1^2+x2^2)+x1x2

=10x1x2+3*23

=69+10*(-7)=-1

a) \(250 + 250 × 2 = 250 + 500 = 750 \\ (250 + 250) × 2 = 500 × 2 = 1 000\)

b)\( 750 – 50 × 5 = 750 – 250 = 500\\ (750 – 50) × 5 = 700 × 5 = 3 500\)
c) \(210 × 4 – 4 × 210 = 840 – 840 = 0\\ 3 × (270 : 9) × 0 = 0\)