Phương trình sau có bao nhiêu nghiệm: 1 + 3 x 2 = 2 x
A. 0 B. 1
C. 2 D. Vô số
Những câu hỏi liên quan
phương trình \(\sqrt{x-5}=\sqrt{3-x}\) có bao nhiêu nghiệm
phương trình \(\sqrt{4x-8}-2\sqrt{\dfrac{x-2}{4}}=3\) có nghiệm là
\(\sqrt{4x-8}-2\sqrt{\dfrac{x-2}{4}}=3\left(x\ge2\right)\\ \Leftrightarrow2\sqrt{x-2}-\sqrt{x-2}=3\\ \Leftrightarrow\sqrt{x-2}=3\Leftrightarrow x-2=9\\ \Leftrightarrow x=11\left(tm\right)\)
Đúng 2
Bình luận (0)
ĐKXĐ: \(x\ge2\)
\(pt\Leftrightarrow2\sqrt{x-2}-\sqrt{x-2}=3\)
\(\Leftrightarrow\sqrt{x-2}=3\Leftrightarrow x-2=9\Leftrightarrow x=11\left(tm\right)\)
Đúng 2
Bình luận (0)
ĐKXĐ: \(3\ge x\ge5\)(vô lý)
Vậy pt vô nghiệm
Đúng 2
Bình luận (0)
có bao nhiêu cặp (a,b) để phương trình sau có nghiệm x∈R : (x-1)(x+2)(ax2+bx+2)≥0
Nguyên tắc xét dấu cơ bản: 1 đa thức (chính xác là biểu thức) luôn đổi dấu khi đi qua nghiệm bội lẻ và không đổi dấu khi đi qua nghiệm bội chẵn. Ở khoảng gần với dương vô cùng (nghĩa là các giá trị x rất lớn), dấu của đa thức luôn trùng với dấu của hệ số bậc cao nhất của biến.
Đặt \(f\left(x\right)=\left(x-1\right)\left(x+2\right)\left(ax^2+bx+2\right)\)
Do \(f\left(x\right)\) luôn có 2 nghiệm \(x=1;x=-2\) nên để \(f\left(x\right)\) không đổi dấu trên R thì đây phải là 2 nghiệm bội chẵn
\(\Rightarrow ax^2+bx+2=0\) có 2 nghiệm \(x=1;x=-2\)
Đồng thời theo nguyên tắc thứ 2 thì \(f\left(x\right)\ge0\) với mọi x khi \(a>0\)
Từ đó ta có hệ điều kiện: \(\left\{{}\begin{matrix}x_1+x_2=1-2=-\dfrac{b}{a}\\x_1x_2=1.\left(-2\right)=\dfrac{2}{a}\\a>0\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại a; b thỏa mãn yêu cầu đề bài
Đúng 2
Bình luận (0)
Phương trình lg4(x - 1) 2 + lg2(x - 1) 3 25 có bao nhiêu nghiệm ? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Phương trình lg4(x - 1) 2 + lg2(x - 1) 3 = 25 có bao nhiêu nghiệm ?
A. 2
B. 3
C. 4
D. 5
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau? 1. Phương trình vô nghiệm trên trường số thực R. 2. Phương trình vô nghiệm trên trường số phức C 3. Phương trình không có nghiệm thuộc tập số thực. 4. Phương trình có bốn nghiệm thuộc tập số phức. 5. Phương trình chỉ có hai nghiệm là số phức. 6. Phương trình có hai nghiệm là số thực A. 0. B. 1. C. 3. D. 2.
Đọc tiếp
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
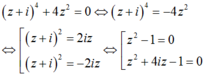
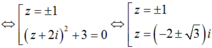
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Đúng 0
Bình luận (0)
Phương trình
2
-
f
(
x
)
f
(
x
)
có tập nghiệm
T
1
20
;
18
;
3
. Phương trình
2
g...
Đọc tiếp
Phương trình 2 - f ( x ) = f ( x ) có tập nghiệm T 1 = 20 ; 18 ; 3 . Phương trình 2 g ( x ) - 1 + 3 g ( x ) - 2 3 = 2 g ( x ) có tập nghiệm T 2 = 0 ; 3 ; 15 ; 19 . Hỏi tập nghiệm của phương trình f ( x ) g ( x ) + 1 = f ( x ) + g ( x ) có bao nhiêu phần tử?
A. 4
B. 3
C. 11
D. 6
Bài 1: Phương trìnhlog_{2} ^3(x-1)-27y^3+8^y+1-x có bao nhiêu (x;y) nghiệm thuộc [8^{1992}; 8^{2020}]Bài 2: Tìm tập hợp số thực m để phương trình 2^{2x-1}+m×2^x+2m-20 có 2 nghiệm thực phân biệt thuộc đoạn [1;2]Bài 3: Tìm các số nguyên m để phương trình log_{dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{dfrac{1}{2}}dfrac{1}{x-2}+4m-4 có nghiệm thuộc [dfrac{5}{2};4]Bài 4: Cho phương trình (m-2)×log_{2} ^2 (x-4)-(2m+1)log_{dfrac{1}{2}} (x-4)+m+20. Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn...
Đọc tiếp
Bài 1: Phương trình\(\log_{2} ^3(x-1)-27y^3+8^y+1-x\) có bao nhiêu \((x;y)\) nghiệm thuộc \([8^{1992}; 8^{2020}]\)
Bài 2: Tìm tập hợp số thực m để phương trình \(2^{2x-1}+m×2^x+2m-2=0\) có 2 nghiệm thực phân biệt thuộc đoạn [1;2]
Bài 3: Tìm các số nguyên m để phương trình \(\log_{\dfrac{1}{2}}^{2} (x-2)^3+4(m-5) log _{\dfrac{1}{2}}\dfrac{1}{x-2}+4m-4\) có nghiệm thuộc \([\dfrac{5}{2};4]\)
Bài 4: Cho phương trình \((m-2)×log_{2} ^2 (x-4)-(2m+1)log_{\dfrac{1}{2}} (x-4)+m+2=0.\) Tìm m để phương trình có 2 nghiệm phân biệt x1, x2 thỏa mãn 4<x1, x2<6
phương trình 1-x/x+1+3=x+3/x+1 có bao nhiêu nghiệm
Cho các khẳng định sau:(1) Phương trình |x – 3| 1 chỉ có một nghiệm là x 2(2) Phương trình |x – 1| 0 có 2 nghiệm phân biệt(3) Phương trình |x – 3| 1 có hai nghiệm phân biệt là x 2 và x 4Số khẳng định đúng là: A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Cho các khẳng định sau:
(1) Phương trình |x – 3| = 1 chỉ có một nghiệm là x = 2
(2) Phương trình |x – 1| = 0 có 2 nghiệm phân biệt
(3) Phương trình |x – 3| = 1 có hai nghiệm phân biệt là x = 2 và x = 4
Số khẳng định đúng là:
A. 0
B. 1
C. 2
D. 3
Xét phương trình |x – 3| = 1
TH1: |x – 3| = x – 3 khi x – 3 ≥ 0 ó x ≥ 3
Phương trình đã cho trở thành x – 3 = 1 ó x = 4 (TM)
TH2: |x – 3| = 3 – x khi x – 3 < 0 ó x < 3
Phương trình đã cho trở thanh 3 – x = 1 ó x = 2 (TM)
Vậy phương trình |x – 3| = 1 có hai nghiệm x = 2 và x = 4 hay (1) sai và (3) đúng
|x – 1| = 0 ó x – 1 = 0 ó x = 1 nên phương trình |x – 1| = 0 có nghiệm duy nhất hay (2) sai.
Vậy có 1 khẳng định đúng
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Có bao nhiêu nghiệm nguyên thuộc khoảng (-9;9) của tham số m để bất phương trình sau có nghiệm thực:
3
logx
≤
2
log
m
x
-
x
2
-
(
1...
Đọc tiếp
Có bao nhiêu nghiệm nguyên thuộc khoảng (-9;9) của tham số m để bất phương trình sau có nghiệm thực: 3 logx ≤ 2 log m x - x 2 - ( 1 - x ) 1 - x ?
A. 6.
B. 7.
C. 10.
D. 11.
Phương trình lg(x-3) + lg(x-2) =1- lg5 có tất cả bao nhiêu nghiệm trên tập số thực.
A. 2
B. 3
C . 1
D. 4
Chọn D.
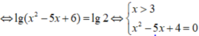
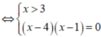
<=> x = 4
Vậy phương trình đã cho có nghiệm duy nhất là x= 4
Đúng 0
Bình luận (0)