\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)

\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)

\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)

\(\Leftrightarrow x^2-9-x^2+3x=0\)

\(\Leftrightarrow3x-9=0\)

\(\Leftrightarrow3x=9\)

\(\Leftrightarrow x=3\left(n\right)\)

Vậy \(S=\left\{3\right\}\)

\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)

\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)

\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)

\(\Leftrightarrow12x-9-12x+20+2x-7>0\)

\(\Leftrightarrow2x+4>0\)

\(\Leftrightarrow2x>-4\)

\(\Leftrightarrow x>-2\)

`a,(2x-5)(12+5x)=0`

\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\12+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\5x=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{12}{5}\end{matrix}\right.\)

`b, (x-3)(x-4)-2(x-3)=0`

`<=>(x-3)(x-4-2)=0`

`<=>(x-3)(x-6)=0`

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)

`c, x(x-1)(x+1)=0`

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

`d, (2x)/3 +(2x-1)/6=0`

`<=> (4x)/6 +(2x-1)/6=0`

`<=> (4x+2x-1)/6=0`

`<=> (6x-1)/6=0`

`<=> 6x-1=0`

`<=> 6x=1`

`<=>x=1/6` ( đề là vậy à bạn )

 a) \(\left(2x-5\right)\left(12+5x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\12+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\5x=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2,5\\x=-2,4\end{matrix}\right.\)

b) \(\left(x-3\right)\left(x-4\right)-2\left(x-3\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left[\left(x-4\right)-2\right]=0\)

\(\Leftrightarrow\left(x-3\right)\left(x-6\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=6\end{matrix}\right.\)

c) \(x\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=0\end{matrix}\right.\)

d) \(\dfrac{2x}{3}+\dfrac{2x-1}{6}=0\)

\(\Leftrightarrow\dfrac{4x+2x-1}{6}=0\)

\(\Leftrightarrow6x-1=0\)

\(\Leftrightarrow6x=1\Leftrightarrow x=\dfrac{1}{6}\)

giúp mik với

1. 4x-12=0

<=>4x=12

<=>x=3

2.  x.(x+1)-(x+2)(x+3)=7

<=>x²+x-x²-3x-2x-6=7

<=>x²-x²+x-2x-3x=7+6

<=>-4x=13

<=>x=\(-\dfrac{13}{4}\)

3.   7+2x=22-3x

<=>2x+3x=22-7

<=>5x=15

<=>x=3

4.  (x-1)-(2x-1)=9-x

<=>x-1-2x+1=9-x

<=>x-2x+x=9+1-1

<=>0x=9

vô nghiệm

a) \(x-2=0\Leftrightarrow x=2\)

b) \(x^2-2x=0\Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

e) \(2x^2+5x+3=0\Leftrightarrow\left(2x+3\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=-1\end{matrix}\right.\)

f) \(x^2-x-12=0\Leftrightarrow\left(x-4\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)

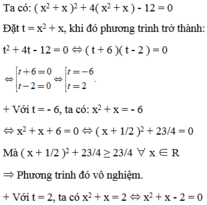
⇔ ( x + 2 )( x - 1 ) = 0 ⇔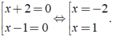 

Vậy phương trình có tập nghiệm là S = { - 2;1 }.

a) \(2x-10=0\)

\(\Leftrightarrow2x=10\)

\(\Leftrightarrow x=5\)

Vậy tập nghiệm của phương trình là: S = {5}

b) \(3,4-x=-4\)

\(\Leftrightarrow x=7,4\)

Vậy tập nghiệm của phương trình là: S = {7,4}

c) \(x-\frac{4}{5}=\frac{1}{5}\)

\(\Leftrightarrow x=1\)

Vậy tập nghiệm của phương trình là: S = {1}

d) \(2\left(x-3\right)-3x+5=0\)

\(\Leftrightarrow2x-6-3x+5=0\)

\(\Leftrightarrow-x-1=0\)

\(\Leftrightarrow x=-1\)

Vậy tập nghiệm của phương trình là: S = {-1}

a, \(2x-10=0\Leftrightarrow x=5\)

Vậy tập nghiệm của phương trình là S = {5}

b, \(3,4-x=-4\Leftrightarrow x=7,4\)kết luận tương tự như trên và các phần còn lại 

c, \(\frac{x-4}{5}=\frac{1}{5}\)Khử mẫu : \(x-4=1\Leftrightarrow x=5\)

d, \(x+12=2-x\Leftrightarrow2x=-10\Leftrightarrow x=-5\)

e, \(2\left(x-3\right)-3x+5=0\Leftrightarrow2x-6-3x+5=0\)

\(\Leftrightarrow-x-1=0\Leftrightarrow x=-1\)

tham khảo

x^2-25=0
x^2=0+25
x^2=25
x=25/2

x(x-3)+4x-12=0
x(x-3)+(4x-12)=0
x(x-3)+4(x-3)=0
(x-3)(x+4)=0
=> x-3=0  => x=3
=> x+4=0    => x= -4