Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng: SAGB = SAGC = SBGC
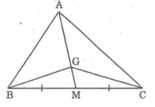
Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng: SAGC = 2SGMC
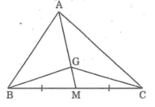
Vì G là trọng tâm của ΔABC nên GA = 2GM (tính chất đường trung tuyến)
Ta có ΔAGC và ΔGMC có chung đường cao kẻ từ đỉnh C đến AM, đồng thời cạnh đáy GA = 2GM.
Suy ra: SAGC = 2SGMC (1)
Cho hình sau trong đó G là trọng tâm của tam giác ABC. Chứng minh rằng: SGMB = SGMC
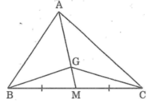
Ta có ΔGMB và ΔGMC có cạnh đáy MB = MC, chung đường cao kẻ từ đỉnh G đến cạnh BC
Suy ra: SGMB = SGMC (2)
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của hai tam giác ABC và A’B’C’.
a) Chứng minh rằng tứ giác AGG’A’ là hình bình hành.
b) Chứng minh rằng AGC.A’G’C’ là hình lăng trụ.
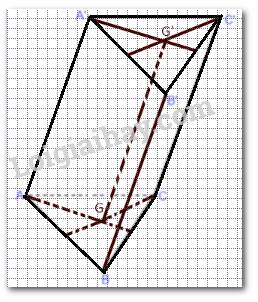
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.
cho hình tứ diện ABCD. Gọi M là điểm trên cạnh AD sao cho MA = 2MD
a, G là trọng tâm tam giác ABD. Chứng minh rằng: MG // (BCD)
b, H là trọng tâm tam giác ABC. Chứng minh rằng: HG // (BCD)
a: Gọi giao điểm của AG với BC là E
Xét ΔABD có
G là trọng tâm
E là giao điểm của AG với BD
Do đó: E là trung điểm của BD và AG=2/3AE
Xét ΔAHD có \(\dfrac{AG}{AE}=\dfrac{AM}{AD}=\dfrac{2}{3}\)
nên GM//ED
=>GM//BD
mà BD\(\subset\left(BCD\right)\) và GM không thuộc mp(BCD)
nên GM//(BCD)
b: Gọi giao của AH với BC là F
Xét ΔABC có
H là trọng tâm
F là giao điểm của AH với BC
Do đó: F là trung điểm của BC và AH=2/3AF
Xét ΔAGE có \(\dfrac{AH}{AF}=\dfrac{AG}{AE}=\dfrac{2}{3}\)
nên HG//FE
mà \(FE\subset\left(BCD\right)\);HG không thuộc(BCD)
nên HG//(BCD)
Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều 3 đỉnh của tam giác đó.
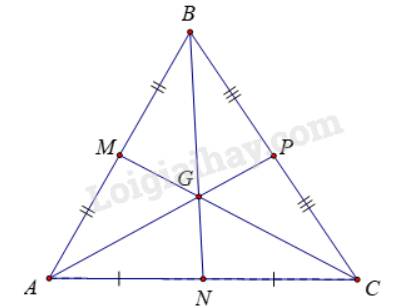
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại B có BN là đường trung tuyến
\( \Rightarrow BN\)là đường trung trực của đoạn thẳng AC
Tam giác BAC cân tại A có AP là đường trung tuyến
\( \Rightarrow AP\)là đường trung trực của đoạn thẳng BC
Mà \(BN \cap AP = G\)
\( \Rightarrow G\)là giao điểm ba đường trung trực của tam giác ABC
\( \Rightarrow GA = GB = GC\).
Cho \(G\) là trọng tâm tam giác \(ABC\), \(M\) là trung điểm \(BC\) và hình chiếu song song của tam giác \(ABC\) là tam giác \(A'B'C'\). Chứng minh rằng hình chiếu \(M'\) của \(M\) là trung điểm của \(B'C'\) và hình chiếu \(G'\) của \(G\) cũng là trọng tâm tam giác \(A'B'C'\).
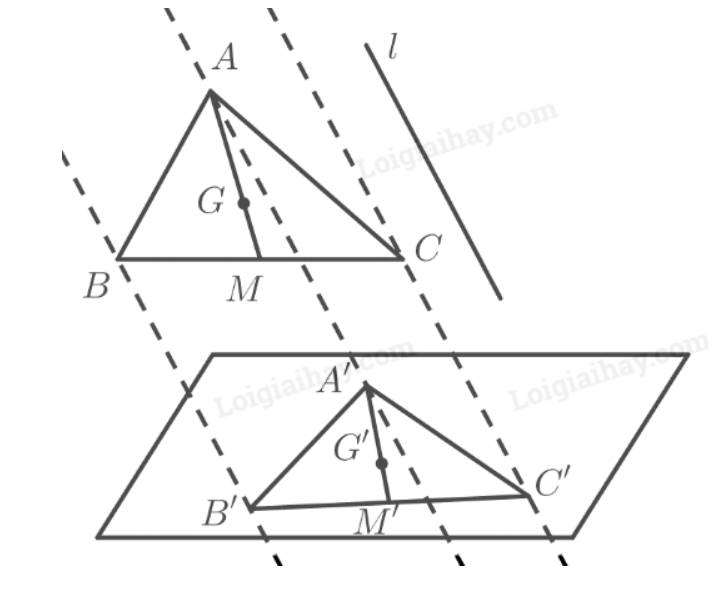
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(M\) nằm giữa \(B\) và \(C\) thì \(M'\) nằm giữa \(B'\) và \(C'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(MB = MC\) thì \(M'B' = M'C'\).
Vậy \(M'\) là trung điểm của \(B'C'\).
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có \(G\) nằm giữa \(A\) và \(M\) thì \(G'\) nằm giữa \(A'\) và \(M'\).
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có \(AG = \frac{2}{3}AM\) thì \(A'G' = \frac{2}{3}A'M'\).
Vậy \(G'\) là trọng tâm tam giác \(A'B'C'\).
Cho tam giác ABC có trung tuyến AM. Lấy điểm G trên AM sao cho AG = 2GM
a) Chứng minh rằng G là trọng tâm của tam giác ABC
b) Gọi D, E, F lần lượt là hính chiếu của G trên các cạnh BC, CA, AB. Chứng minh rằng G cũng là trọng tâm của tam giác DEF
Cho G là trọng tâm của Tam giác đều ABC. Trên tia AG lấy K sao cho G là trung điểm của AK. Chứng minh rằng BGK là tam giác đều.
Vẽ hình giùm mik đi ạ
Đặt \(AB=BC=CA=a\)
Gọi D là trung điểm BC \(\Rightarrow AG=BG=\dfrac{2}{3}AD\) và \(DG=\dfrac{1}{3}AD\)
G là trung điểm AK \(\Rightarrow GK=AG=\dfrac{2}{3}AD\Rightarrow GK=BG\) (1)
\(DG+DK=GK\Rightarrow DK=GK-DG=\dfrac{1}{3}AD\Rightarrow DK=DG\) \(\Rightarrow\) BD là trung tuyến của tam giác BGK
Mặt khác tam giác ABC đều \(\Rightarrow AD\perp BC\) \(\Rightarrow\) BD là đường cao của tam giác BGK
Xét tam giác BGK có BD đồng thời là trung tuyến và đường cao
\(\Rightarrow\Delta BGK\) cân tại B \(\Rightarrow BG=BK\) (2)
Từ (1), (2) \(\Rightarrow BG=BK=GK\Rightarrow\Delta BGK\) là tam giác đều

Cho tam giác ABC nội tiếp trong đường tròn tâm O. Gọi G và H theo thứ tự là trọng tâm và trực tâm của tam giác. Chứng minh rằng
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\)
Từ đó chứng minh G,H, O thẳng hàng.
Đặt \(\overrightarrow{u}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}-\overrightarrow{OH}\)
Ta sẽ chứng minh \(\overrightarrow{u}=\overrightarrow{O}\)
Gọi A1, B1, C1 theo thứ tự là hình chiếu của A, B, C ( cũng là hình chiếu của H) trên các đường thẳng BC, CA, AB và gọi Ao, Bo, Co theo thứ tự là trung điểm BC, CA, AB (như hình vẽ)
Chiếu vectơ \(\overrightarrow{u}\) lên đường thẳng BC theo phương của \(\overrightarrow{AH}\) ta được
\(\overrightarrow{u_a}=\overrightarrow{A_oA_1}+\overrightarrow{A_oB}+\overrightarrow{A_oC}-\overrightarrow{A_oA_1}=\overrightarrow{O}\)
Suy ra \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{AH}\) (1)
Tương tự như vậy,
ta cũng có \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{BH,}\overrightarrow{CH}\) (2)
Từ (1) và (2) và do các vectơ \(\overrightarrow{AH,}\), \(\overrightarrow{BH},\overrightarrow{CH}\) đôi một không cùng phương suy ra \(\overrightarrow{u}=\overrightarrow{O}\)
Vậy \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH}\)
Nhưng \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}\) nên \(\overrightarrow{OH}=3\overrightarrow{OG}\)
Do đó G, H, O thẳng hàng