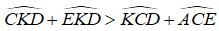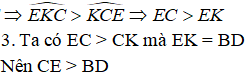Bài tập 6: Cho tam giác ABC có BC = 2BA. BD là đường phân giác. Chứng minh : CD = 2DA.

Những câu hỏi liên quan
Cho tam giác ABC có BC = 2BA . BD là phân giác của tam giác ABC . Chứng minh DC = 2DA
Cho tam giác ABC , BC = 2BA . BD là tia phân giác của tam giác ABC . Chứng minh DC = 2DA
Cho tg ABC có BC = 2BA. Tia phân giác BD. CMR DC = 2DA
Cho \(\Delta ABC\)có \(BC=2BA\). \(BD\)là đường phân giác của \(\Delta ABC\). Chứng minh \(DC=2DA\)
Cho tam giác ABC có BC = 2BA . BD là phân giác của tam giác ABC . Chứng minh DC = 2DA
Đúng 0
Bình luận (0)
Bài 4: Cho tam giác ABC, D nằm trên đoạn BC thỏa mãn: BD/CD=AB/AC. Chứng minh rằng AD là đường phân giác của tam giác ABC.
*Qua C, kẻ đường thẳng song song với AB cắt AD tại E.
- Xét △ABD có: \(AB\)//\(CE\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{BD}{CD}\) (định lí Ta-let).
Mà \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\) (gt)
=>\(\dfrac{AB}{CE}=\dfrac{AB}{AC}\) hay \(CE=AC\).
=>△ACE cân tại C.
=>\(\widehat{EAC}=\widehat{AEC}\).
Mà\(\widehat{AEC}=\widehat{BAD}\) ( \(AB\)//\(CE\) và so le trong).
=>\(\widehat{EAC}=\widehat{BAD}\) hay AD là phân giác của \(\widehat{BAC}\).
Đúng 3
Bình luận (1)
Xét tg ABC có
\(\dfrac{BD}{CD}=\dfrac{AB}{AC}\left(gt\right)\)
=>AD là đường phân giác
Đúng 1
Bình luận (3)
Xem thêm câu trả lời
Bài 3: Cho tam giác ABC vuông tại A có BC 20 cm, AC 16 cm. Vẽ đường cao AH.a) Chứng minh: HBA ABC; HBA HAC.b) Chứng minh: AB2 BH. BC; AH2 HB.HCc) Tính AB, AH, BH.d) Vẽ đường phân giác AD của tam giác ABC (D BC). Tính BD, CD. (Kết quả làm tròn đến chữ số thập phân thứ nhất).e*) Trên AH lấy điểm K sao cho AK 3,6cm. Từ K kẻ đường thẳng song song với BC, cắt AB và AC lần lượt tại M và N. Tính diện tích tứ giác BMNC.
Đọc tiếp
Bài 3: Cho tam giác ABC vuông tại A có BC = 20 cm, AC = 16 cm. Vẽ đường cao AH.
a) Chứng minh: HBA ABC; HBA HAC.
b) Chứng minh: AB2 = BH. BC; AH2 = HB.HC
c) Tính AB, AH, BH.
d) Vẽ đường phân giác AD của tam giác ABC (D BC). Tính BD, CD. (Kết quả làm tròn đến chữ số thập phân thứ nhất).
e*) Trên AH lấy điểm K sao cho AK = 3,6cm. Từ K kẻ đường thẳng song song với BC, cắt AB và AC lần lượt tại M và N. Tính diện tích tứ giác BMNC.
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC
Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AH^2=HB\cdot HC\end{matrix}\right.\)(hệ thức lượng)
c: \(AB=\sqrt{BC^2-AC^2}=12\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)
\(BH=\sqrt{AB^2-AH^2}=7.2\left(cm\right)\)
Đúng 1
Bình luận (0)
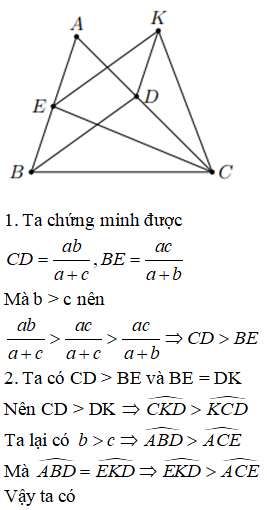
Bài 23/ Cho tam giác ABC có BC = a, AC = b, AB = c (b > c), các đường phân giác BD,
CE.
a) Tính các độ dài CD, BE rồi suy ra CD > BE
b) Vẽ hình bình hành BEKD. Chứng minh CE > EK
c) Chứng minh CE > BD.
Cho tam giác ABC có BC = 2BA . BD là phân giác của tam giác ABC . Chứng minh DC = 2DA
Xét ΔBAC có BD là phân giác
nên DA/DC=BA/BC=1/2
=>DC=2DA
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB AC . Vẽ đường phân giác CD của tam giác ABC. Kẻ BK vuông góc với CD ( K thuộc đường thẳng CD)
a) giả sử AC 24 cm, BC 30 cm. Tính BD / AD
b) vẽ AH là đường cao của tam giác ABC. Chứng minh tam giác HBA và tam giác ABC đồng dạng.
c) chứng minh DA.DBDK.DC
d) trên đoạn thẳng DC lấy điểm F sao cho BF BA. Gọi E là giao điểm của hai đường thẳng HA và BK. Chứng minh BF vuông góc với FE
Đọc tiếp
Cho tam giác ABC vuông tại A có AB < AC . Vẽ đường phân giác CD của tam giác ABC. Kẻ BK vuông góc với CD ( K thuộc đường thẳng CD) a) giả sử AC = 24 cm, BC = 30 cm. Tính BD / AD b) vẽ AH là đường cao của tam giác ABC. Chứng minh tam giác HBA và tam giác ABC đồng dạng. c) chứng minh DA.DB=DK.DC d) trên đoạn thẳng DC lấy điểm F sao cho BF = BA. Gọi E là giao điểm của hai đường thẳng HA và BK. Chứng minh BF vuông góc với FE
a: BD/AD=BC/AC=5/4
b: Xét ΔHBA và ΔABC có
góc BHA=góc BAC
góc B chung
=>ΔHBA đồng dạng với ΔABC
c: Xét ΔDAC và ΔDKB có
góc DAC=góc DKB
góc ADC=góc KDB
=>ΔDAC đồng dạng với ΔDKB
=>DA/DK=DC/DB
=>DA*DB=DK*DC
Đúng 1
Bình luận (0)