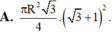
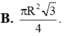
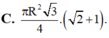
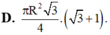
Cho tam giác ABC nội tiếp đường O bán kính R. H là trực tâm của tam giác ABC. Gọi AD la đường kính của đường tròn O

A. CMR : BH = DC

B. CMR : H,G,O thẳng hàng.trong đó G là trong tâm tam giác ABC

C. AH căt (O;R) tại H'. Tinh bán kính đường tròn ngoại tiếp tam giác BH'C

Bai1: Cho tam giác ABC nội tiếp đường tròn tâm O bán kính R. Các đỉnh B, C cố định còn A chạy trên đường tròn đó. Tìm tập hợp các trọng tâm G của tam giác ABC khi A di độngCho tam giác ABC nội tiếp đường tròn tâm O bán kính R. các bạn giúp mih` giải và vẽ hình bài này nhé help me đang cần gấp

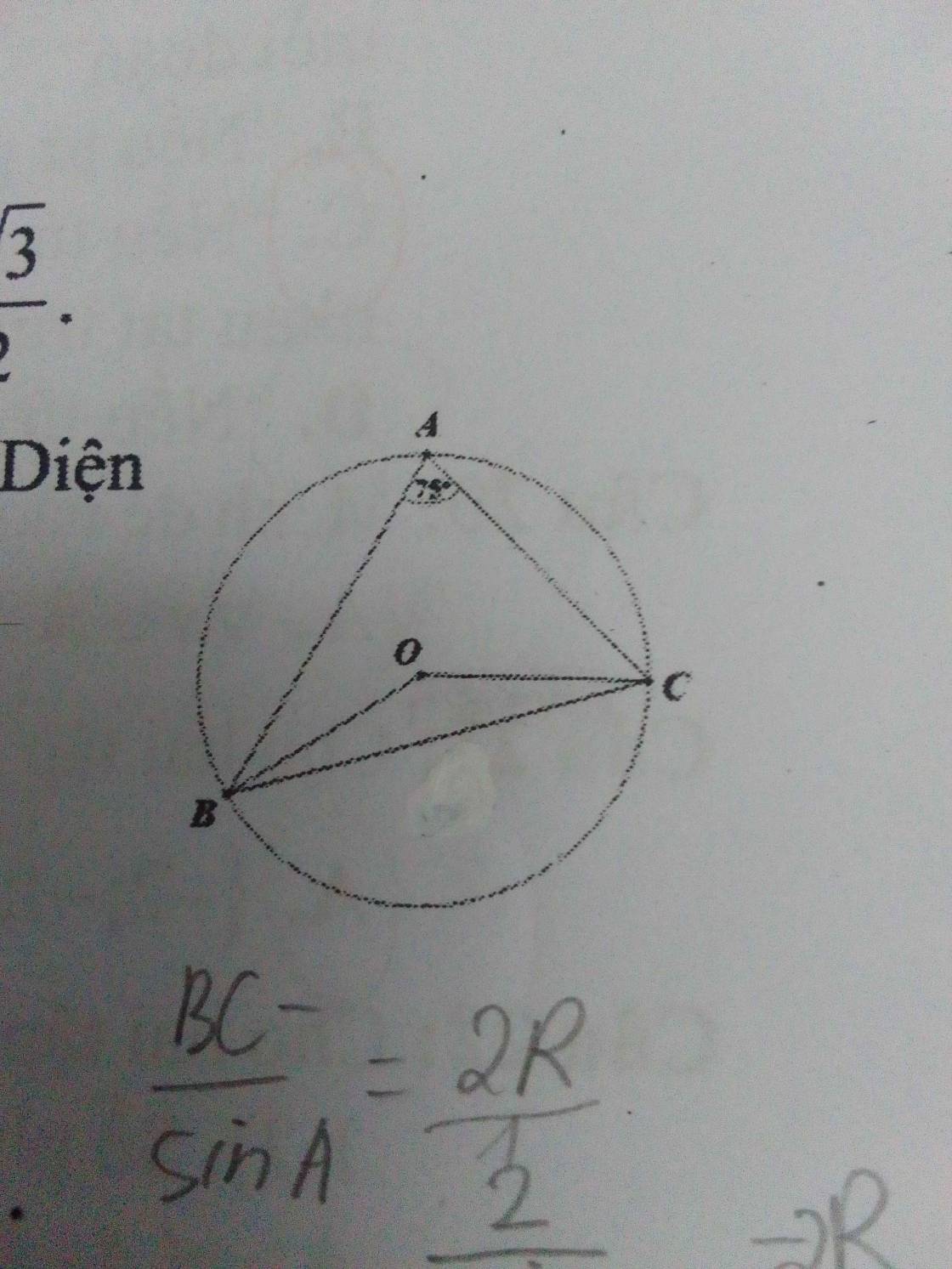  Cho tam giác ABC, góc A=75° nội tiếp đường tròn tâm O bán kính R=1. tính diện tích tam giác OBC.

Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số \(\dfrac{R}{r}\) bằng

Giải chi tiết cho mk vs

Tam giác ABC vuông tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Kho đó tỉ số R/r bằng

 

cho tam giác abc  nội tiếp đường tròn (O;R) bán kính R trong đó B,C cố đinhj chứng minh rằng trọng tâm g của tam giác luôn thuộc một ddường tròn cố định

cho tam giác ABC có AB=AC=40, BC=48. gọi O và I thứ tự là tâm đường tròn ngoại tiếp tam và nội tiếp tam giác. tính
a) Bán kính đường tròn nội tiếp
b) Bán kính đường tròn ngoại tiếp
c) Khoảng cách OI

Cho đường tròn tâm O bán kính R có đường kính AB, dây cung BC=R.

a) Tính AC theo R và số đo góc B của tam giác ABC.

b) Đường thẳng qua O vuông góc với AC cắt tiếp tuyến tại A của đường tròn tâm O ở D.

Chứng minh DC là đường tiếp tuyến của đường tròn tâm O.

c) Đường thẳng OD cắt đường tròn tâm O tại I. Chứng minh rằng I là tâm đường tròn nội tiếp tam giác ADC.