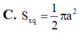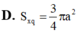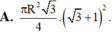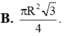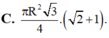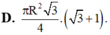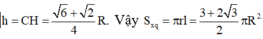Các câu hỏi tương tự
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có
B
A
C
^
75
0
,
A
C
B
^
60
0
. Kẻ BH
⊥
AC. Quay quanh AC thì
∆
BHC tạo...
Đọc tiếp
Cho tam giác ABC nội tiếp trong đường tròn tâm O, bán kính R có B A C ^ = 75 0 , A C B ^ = 60 0 . Kẻ BH ⊥ AC. Quay quanh AC thì ∆ BHC tạo thành hình nón tròn xoay (N). Tính diện tích xung quanh của hình nón xoay (N) theo R.
A. 3 + 2 2 2 πR 2
B. 3 + 2 3 2 πR 2
C. 3 ( 1 + 2 ) 4 πR 2
D. 3 ( 1 + 3 ) 4 πR 2
Cho tam giác ABC vuông tại B có AC2a, BCa khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
Đọc tiếp
Cho tam giác ABC vuông tại B có AC=2a, BC=a khi quay tam giác ABC quay quanh cạnh góc vuông AB thì đường gấp khúc ABC tạo thành một hình nón tròn xoay có diện tích xung quanh bằng
![]()
![]()
![]()
![]()
Cho tam giác ABC nội tiếp đường tròn (O;R). Điểm A cố định, dây BC có độ dài bằng R, G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu? A.
R
3
B.
R
3
2
C.
R
3
3
D.
R
2
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O;R). Điểm A cố định, dây BC có độ dài bằng R, G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu?
A. R 3
B. R 3 2
C. R 3 3
D. R 2
Trong không gian cho tam giác ABC vuông tại A có AB a, AC
a
3
. Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AB. A. l
a
3
B. l
a
2
C. l
(
1
+
3
)
a
D. l 2a
Đọc tiếp
Trong không gian cho tam giác ABC vuông tại A có AB = a, AC = a 3 . Tính độ dài đường sinh l của hình nón nhận được khi quay tam giác ABC xung quanh trục AB.
A. l = a 3
B. l= a 2
C. l = ( 1 + 3 ) a
D. l = 2a
Cho tam giác AOB vuông tại O, có
O
A
B
^
30
0
và AB a. Quay tam giác AOB quanh trục AO ta được một hình nón. Tính diện tích xung quanh
S
x
q
của hình nón đó. A.
S
x
q
...
Đọc tiếp
Cho tam giác AOB vuông tại O, có O A B ^ = 30 0 và AB = a. Quay tam giác AOB quanh trục AO ta được một hình nón. Tính diện tích xung quanh S x q của hình nón đó.
A. S x q = πa 2 2
B. S x q = πa 2
C. S x q = πa 2 4
D. S x q = 2 πa 2
Cho tam giác AOB vuông tại O và OAB
30
o
Đường cao hạ từ O là OH,OHa Tính thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA.
Đọc tiếp
Cho tam giác AOB vuông tại O và OAB= 30 o Đường cao hạ từ O là OH,OH=a Tính thể tích khối nón tròn xoay tạo bởi tam giác AOB khi quay quanh trục OA.
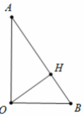
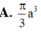
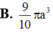
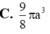
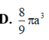
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh
S
x
p
của hình nón đó. A.
π
a
2
B.
1
2
π
a
2
C.
3
4
π...
Đọc tiếp
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh S x p của hình nón đó.
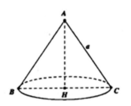
A. π a 2
B. 1 2 π a 2
C. 3 4 π a 2
D. 2 π a 2
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tam giác AGC quay quanh AG tạo thành một khối tròn xoay có thể tích là:
A
.
πa
3
3
36
B
.
πa
3
3
12
C
.
...
Đọc tiếp
Cho tam giác ABC đều cạnh bằng a, trọng tâm G. Tam giác AGC quay quanh AG tạo thành một khối tròn xoay có thể tích là:
A . πa 3 3 36
B . πa 3 3 12
C . πa 3 3 24
D . πa 3 3 18
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh
S
x
q
của hính nón đó.
Đọc tiếp
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Tính diện tích xung quanh S x q của hính nón đó.
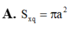
![]()